题目内容
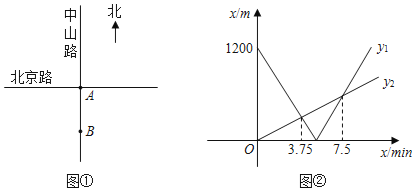
【题目】如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点
．甲从中山路上点
出发，骑车向北匀速直行；与此同时，乙从点出发，沿北京路步行向东匀速直行．设出发
时，甲、乙两人与点的距离分别为
、
．已知
、
与
之间的函数关系如图②所示．
（1）求甲、乙两人的速度；
（2）当取何值时，甲、乙两人之间的距离最短？
【答案】（1）甲的速度为
，乙的速度为
．（2）当
时，甲、乙两人之间的距离最短．
【解析】
(1)设甲、乙两人的速度，并依题意写出函数关系式，再根据图②中函数图象交点列方程组求解；
(2)设甲、乙之间距离为
，由勾股定理可得
，根据二次函数最值即可得出结论．
(1)设甲、乙两人的速度分别为
，
，甲从B到A用时为p分钟，则：
，
，
由图②知： 
或
时，
，
则有
，解得： 
，
p=1200÷240=5，
答：甲的速度为，乙的速度为；
(2)设甲、乙之间距离为，
则
，
当时，
的最小值为
，即的最小值为
，
答：当时，甲、乙两人之间的距离最短．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
