题目内容
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 可以由
可以由![]() 绕点
绕点![]() 顺时针旋转得到,其中点
顺时针旋转得到,其中点![]() 与点
与点![]() 是对应点,点
是对应点,点![]() 与点
与点![]() 是对应点,连接
是对应点,连接![]() ,且
,且![]() 、
、![]() 、
、![]() 在同一条直线上,则
在同一条直线上,则![]() 的长为( )
的长为( )
A.6B.![]() C.
C.![]() D.3
D.3
【答案】A
【解析】
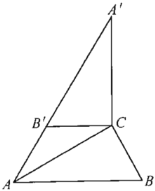
先利用互余计算出∠BAC=30°,再根据含30度的直角三角形三边的关系得到AB=2BC=4,接着根据旋转的性质得A'B'=AB=4,B'C=BC=2,A'C=AC,∠A'=∠BAC=30°,∠A'B'C=∠B=60°,于是可判断△CAA'为等腰三角形,所以∠CAA'=∠A'=30°,再利用三角形外角性质计算出∠B'CA=30°,可得B'A=B'C=2,然后利用AA'=AB'+A'B'进行计算.
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∴AB=2BC=2×2=4.
∵△ABC绕点C顺时针旋转得到△A'B'C',
∴A'B'=AB=4,B'C=BC=2,A'C=AC,∠A'=∠BAC=30°,∠A'B'C=∠B=60°,
∴△CAA'为等腰三角形,
∴∠CAA'=∠A'=30°.
∵A、B'、A'在同一条直线上,
∴∠A'B'C=∠B'AC+∠B'CA,
∴∠B'CA=60°﹣30°=30°,
∴B'A=B'C=2,
∴AA'=AB'+A'B'=2+4=6.
故选:A.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目