题目内容
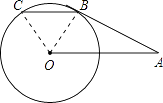
【题目】如图,AB切⊙O于点B,BC∥OA,交⊙O于点C,若∠OAB=30°,BC=6,则劣弧BC的长为 . 
【答案】2π
【解析】解:连接OB,OC,
∵AB为圆O的切线,
∴∠ABO=90°,
在Rt△ABO中,∠OAB=30°,
∴∠AOB=60°,
∵BC∥OA,
∴∠OBC=∠AOB=60°,
又∵OB=OC,
∴△BOC为等边三角形,
∴∠BOC=60°,BO=CO=BC=6,
则劣弧BC长= ![]() =2π.
=2π.
答案为:2π.
【考点精析】本题主要考查了切线的性质定理和弧长计算公式的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.