Question

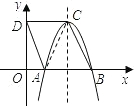
如图，四边形ABCD是菱形，点D的坐标是（0，

3

），以点C为顶点的抛物线y=ax²+bx+c恰经过x轴上的点A，B．
（1）求点C的坐标；
（2）若抛物线向上平移后恰好经过点D，求平移后抛物线的解析式．

Answer 1

（1）连接AC，在菱形ABCD中，CD∥AB，
AB=BC=CD=DA，
由抛物线对称性可知AC=BC．（1分）
∴△ABC，△ACD都是等边三角形．
∴CD=AD=

OD

sin60°

=2（2分）
∴点C的坐标为（2，

3

）．（3分）

（2）由抛物线y=ax²+bx+c的顶点为（2，

3

），
可设抛物线的解析式为．y=a(x-2)2+

3

由（1）可得A（1，0），把A（1，0）代入上式，
解得a=-

3

．（5分）
设平移后抛物线的解析式为y=-

3

（x-2）²+k，
把（0，

3

）代入上式得K=5

3

．
∴平移后抛物线的解析式为：
y=-

3

（x-2）²+5

3

（7分）
即y=-

3

x²+4

3

x+

3

．