题目内容
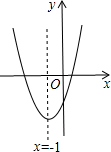
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列5个结论:
①abc<0;②a+c>b;③4a+2b+c>0;④c>-2a;⑤a+b>am2+bm(m≠1).
其中正确的结论有______(填序号).

①abc<0;②a+c>b;③4a+2b+c>0;④c>-2a;⑤a+b>am2+bm(m≠1).
其中正确的结论有______(填序号).

①正确,由函数图象开口向下可知,a<0,由图象与y轴的交点在y轴的正半轴可知,c>0,由函数的对称轴x=-
=1>0,a<0,可知,b>0,故abc<0;
②错误,因为x=-
=
=1,x=-1,故x=-1时,y=a+b+c=0,即a+c=b;
③正确,由函数图象可知对称轴x=-
=1,所以2a=-b,即4a=-2b,故4a+2b=0,
因为c>0,所以4a+2b+c>0;
④正确,由函数图象的对称轴及与x轴的一个交点为3可知,与x轴的另一个交点为-1,故x1x2=
=-3,
∴c=-3a,∵a<0,∴c>-2a;
⑤正确,∵当x=1时,y=a+b+c,
当x=m时,y=am2+bm+c,
∵当x=1时,y取最大值,
∴a+b+c>am2+bm+c(m≠1),
∴a+b>am2+bm(m≠1).
故填①③④⑤.
| b |
| 2a |
②错误,因为x=-
| b |
| 2a |
| x+3 |
| 2 |
③正确,由函数图象可知对称轴x=-
| b |
| 2a |
因为c>0,所以4a+2b+c>0;
④正确,由函数图象的对称轴及与x轴的一个交点为3可知,与x轴的另一个交点为-1,故x1x2=
| c |
| a |
∴c=-3a,∵a<0,∴c>-2a;
⑤正确,∵当x=1时,y=a+b+c,
当x=m时,y=am2+bm+c,
∵当x=1时,y取最大值,
∴a+b+c>am2+bm+c(m≠1),
∴a+b>am2+bm(m≠1).
故填①③④⑤.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 轴上的点A,B.
轴上的点A,B.
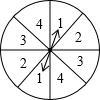 的机会的大小,但没有转盘,请你为小华找三种不同的满足条件的替代物作模拟实验.实物替代物:
的机会的大小,但没有转盘,请你为小华找三种不同的满足条件的替代物作模拟实验.实物替代物: