题目内容
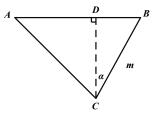
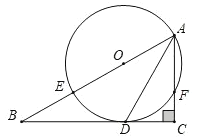
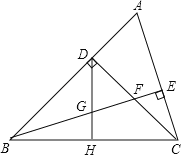
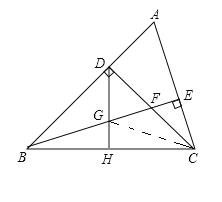
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD交于F,H是BC边的中点,连接DH与BE交于点G,则下列结论:
①BF=AC;②∠A=∠DGE;③CE<BG;④S△ADC=S四边形CEGH;⑤DGAE=DCEF中,正确结论的个数是( )
A.2B.3C.4D.5
【答案】C
【解析】
证明△BDF≌△CDA可判断①;
由![]() 利用三角形的外角的性质及四边形的内角和定理可判断②;
利用三角形的外角的性质及四边形的内角和定理可判断②;
连接![]() 利用DH是BC的垂直平分线,从而可判断③;
利用DH是BC的垂直平分线,从而可判断③;
过G作GJ⊥AB于J,过F作FM![]() BC于M,连接GM,设
BC于M,连接GM,设![]() 分别计算三角形ADC的面积和四边形CEGH的面积可判断④;
分别计算三角形ADC的面积和四边形CEGH的面积可判断④;
由△BDF∽△CEF,可判断⑤.
解:∵CD⊥AB,BF⊥AC,
∴∠BEC=∠BDC=∠ADC=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠ABC,
∴BD=DC,
∵∠BDC=∠CEF=90°,∠DFB=∠EFC,
∴由三角形内角和定理得:∠DBF=∠ACD,
∵在△BDF和△CDA中,
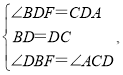
∴△BDF≌△CDA(ASA),
∴BF=AC,∠BFD=∠A,∴①正确;
∵∠DFB=∠FBC+∠FCB=∠FBC+45°,∠DGF=∠GBD+45°,∠FBC=∠GBD,
∴∠DFG=∠DGF,
![]()
![]()
![]()
![]()
∴∠A=∠DGE,故②正确,
如图,连接![]()
∵∠ABC=45°,∠BDC=90°,
∴△BDC是等腰直角三角形,
∵H是BC边的中点,
∴DH垂直平分BC,
![]()
![]()
![]()
![]() 故③正确;
故③正确;
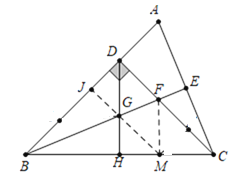
过G作GJ⊥AB于J,过F作FM![]() BC于M,连接GM,
BC于M,连接GM,
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形DGMF是菱形,
四边形DGMF是菱形,
![]()
设![]()
则![]()
![]()
![]() 四边形CFGH的面积=梯形GHMF的面积+
四边形CFGH的面积=梯形GHMF的面积+![]() 的面积
的面积
![]()
![]()
![]() S△ADC
S△ADC![]() S四边形CEGH,故④错误.
S四边形CEGH,故④错误.
∵△BDF∽△CEF,
∴![]() ,
,
∵BD=DC,CE=AE,DF=DG,
∴![]()
∴DGAE=DCEF,故⑤正确.
故选:C.

 阅读快车系列答案
阅读快车系列答案