��Ŀ����
�ţ�1������ѧ����ѧϰС�飬Ϊ���о�ѧϰ���κ������⣬���Ǿ�����ʵ��--Ӧ��--̽���Ĺ��̣�
��1��ʵ�������Ƕ�һ����·�Ϻ����Ϊ�����ߵĵ���˫��������������ͼ�٣����в��������һ������·���Ϊ10m������������ߴ������6.25m������������������ͼ����������ͼ����ʾ��ֱ������ϵ��������������ߵĽ���ʽ��
��2��Ӧ�ã����涨��������ͨ������ʱ����������������������ֱ�����ϵĸ߶Ȳ�����Ϊ0.5m��Ϊ��ȷ����ȫ���ʸ������ܷ������3m�����3.5m��������ʽ�������в�����ʻ������������ʻʱ������������Ŀ�϶����
��3��̽�����ÿ���ѧϰС��Ϊ��һ��̽�������ߵ��й�֪ʶ�����ǽ�������������ģ�ͣ�����������������⣬������
I����ͼ�ۣ�����������������ABCD��ʹ����C��D���ڒ������ϣ�����A��B����x���ϣ������ABCD���ܳ�Ϊl��l�����ֵ��
II����ͼ�ܣ���ԭ����һ��y=x��ֱ��OM�����������ڵ�M���������߶Գ����ڵ�N��P��Ϊֱ��0M��һ���㣬��P����x��Ĵ��߽��������ڵ�Q������ֱ��OM���Ƿ���ڵ�P��ʹ��P��N��QΪ������������ǵ���ֱ�������Σ������ڣ������P������ꣻ�������ڣ���˵�����ɡ�
��1��ʵ�������Ƕ�һ����·�Ϻ����Ϊ�����ߵĵ���˫��������������ͼ�٣����в��������һ������·���Ϊ10m������������ߴ������6.25m������������������ͼ����������ͼ����ʾ��ֱ������ϵ��������������ߵĽ���ʽ��
��2��Ӧ�ã����涨��������ͨ������ʱ����������������������ֱ�����ϵĸ߶Ȳ�����Ϊ0.5m��Ϊ��ȷ����ȫ���ʸ������ܷ������3m�����3.5m��������ʽ�������в�����ʻ������������ʻʱ������������Ŀ�϶����
��3��̽�����ÿ���ѧϰС��Ϊ��һ��̽�������ߵ��й�֪ʶ�����ǽ�������������ģ�ͣ�����������������⣬������
I����ͼ�ۣ�����������������ABCD��ʹ����C��D���ڒ������ϣ�����A��B����x���ϣ������ABCD���ܳ�Ϊl��l�����ֵ��
II����ͼ�ܣ���ԭ����һ��y=x��ֱ��OM�����������ڵ�M���������߶Գ����ڵ�N��P��Ϊֱ��0M��һ���㣬��P����x��Ĵ��߽��������ڵ�Q������ֱ��OM���Ƿ���ڵ�P��ʹ��P��N��QΪ������������ǵ���ֱ�������Σ������ڣ������P������ꣻ�������ڣ���˵�����ɡ�


| �⣺��1����������ϵ��֪�˺�����������Ϊ��5��6.25���� ���������ߵĽ���ʽΪ  �� ����ͼ�����10��0���㣬 ��  �� ����� 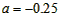 �� ���������ߵĽ���ʽΪ 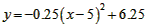 �� �� |
|
| ��2�������3m�����3.5m��������ʽ�������в�����ʻʱ��x=2�� ��x=2�������ʽ�ã�y=-0.25��2-5��2+6.25��y=4�� ��4-3.5=0.5�� �������������3m�����3.5m��������ʽ�������в�����ʻ�� |
|
| ��3��I������AO=x���ɵ�AB=10-2x�� ��AD=-0.25��x-5��2+6.25�� �����ABCD���ܳ�Ϊl�� l=2[-0.25��x-5��2+6.25]+2��10-2x��=-0.5x2+x+20=-0.5��x-1��2+20.5�� ��l�����ֵΪ20.5�� II������P��N��QΪ������������ǵ���ֱ�������Σ� ��P��y=x��ͼ���ϣ���P��m��m���� ��P����x��Ĵ��߽��������ڵ�Q�� ���POA=��OPA=45�㣬N�������Ϊ��5��5���� ��Q�������Ϊ��m��5���� ��Q����������  ���� ����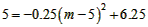 �� ����� 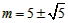 �� ����ʹ��P��N��QΪ������������ǵ���ֱ�������Σ�P�������Ϊ���� 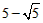 �� ��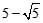 ���� ����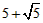 ���� ���� |
 |

��ϰ��ϵ�д�
�����Ŀ
ijУ���꼶��2�����ڲ���У����˸߶ȵ���ѧ��У���һ���ͬѧ��������ֲ��������������ݲ��������д�����¡���ѧ����桷�е�һ���֣�
��1�������ڷ���һ������ѡһ�ַ�������ѡ���ӷ֣������ݷ����ṩ��ʾ��ͼ�����������д���еļ�����̡����������
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��
| ���� | ����У����˸߶� | ||
| Ŀ�� | ������ѧ��ѧ֪ʶ����ѧ�������ʵ������---������˸߶� | ||
| ���� | ����һ | ������ | ������ |
ʾ��ͼ |
 |
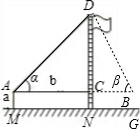 |
|
| �������� | Ƥ�ߡ������ | Ƥ�ߡ������ | |
| �������� | AM=1.5m��AB=10m �Ϧ�=30�㣬�Ϧ�=60�� |
AM=1.5m��AB=20m �Ϧ�=30�㣬�Ϧ�=60�� |
|
| ������̣��� ���������ţ� |
�⣺ | �⣺ | |
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��
ijУ���꼶��2�����ڲ���У����˸߶ȵ���ѧ��У���һ���ͬѧ��������ֲ��������������ݲ��������д�����¡���ѧ����桷�е�һ���֣�
��ѧ�����
�С�飺��һ��
��ص㣺ѧУ�ٳ�
�ʱ�䣺��������������¡�����������9��00
�С���鳤��������
��1�������ڷ���һ������ѡһ�ַ�������ѡ���ӷ֣������ݷ����ṩ��ʾ��ͼ�����������д���еļ�����̡����������
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��
��ѧ�����
�С�飺��һ��
��ص㣺ѧУ�ٳ�
�ʱ�䣺��������������¡�����������9��00
�С���鳤��������
| ���� | ����У����˸߶� | ||
| Ŀ�� | ������ѧ��ѧ֪ʶ����ѧ�������ʵ������----������˸߶� | ||
| ���� | ����һ | ������ | ������ |
ʾ��ͼ |
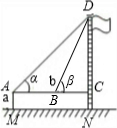 |
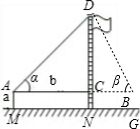 |
|
| �������� | Ƥ�ߡ������ | Ƥ�ߡ������ | |
| �������� | AM=1.5m��AB=10m �Ϧ�=30�㣬�Ϧ�=60�� |
AM=1.5m��AB=20m �Ϧ�=30�㣬�Ϧ�=60�� |
|
| ������̣��� ���������ţ� |
�⣺ |
�⣺ | |
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��
ijУ���꼶��2�����ڲ���У����˸߶ȵ���ѧ��У���һ���ͬѧ��������ֲ��������������ݲ��������д�����¡���ѧ����桷�е�һ���֣�
��ѧ�����
�С�飺��һ�� ��ص㣺ѧУ�ٳ�
�ʱ�䣺��������������¡�����������9��00 �С���鳤��������
��ѧ�����
�С�飺��һ�� ��ص㣺ѧУ�ٳ�
�ʱ�䣺��������������¡�����������9��00 �С���鳤��������
| ���� | ����У����˸߶� |
| Ŀ�� | ������ѧ��ѧ֪ʶ����ѧ�������ʵ������--������˸߶� |
| ʾ��ͼ | 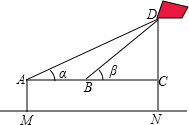 |
| �������� | Ƥ�ߡ������ |
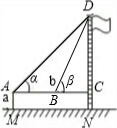
| �������ݣ� | AM=1.5m��AB=10m���Ϧ�=30�㣬�Ϧ�=60�� |
| ������̣��� ���������ţ� |
�⣺ |
| ������� | DN= |
ijУ���꼶��2�����ڲ���У����˸߶ȵ���ѧ��У���һ���ͬѧ��������ֲ��������������ݲ��������д�����¡���ѧ����桷�е�һ���֣�
��ѧ�����
�С�飺��һ��
��ص㣺ѧУ�ٳ�
�ʱ�䣺��������������¡�����������9��00
�С���鳤��������
| ���� | ����У����˸߶� | ||
| Ŀ�� | ������ѧ��ѧ֪ʶ����ѧ�������ʵ������----������˸߶� | ||
| ���� | ����һ | ������ | ������ |
ʾ��ͼ |  |  | |
| �������� | Ƥ�ߡ������ | Ƥ�ߡ������ | |
| �������� | AM=1.5m��AB=10m �Ϧ�=30�㣬�Ϧ�=60�� | AM=1.5m��AB=20m �Ϧ�=30�㣬�Ϧ�=60�� | |
| ������̣��� ���������ţ� | �⣺ | �⣺ | |
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��
ijУ���꼶��2�����ڲ���У����˸߶ȵ���ѧ��У���һ���ͬѧ��������ֲ��������������ݲ��������д�����¡���ѧ����桷�е�һ���֣�
��1�������ڷ���һ������ѡһ�ַ�������ѡ���ӷ֣������ݷ����ṩ��ʾ��ͼ�����������д���еļ�����̡����������
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��
| ���� | ����У����˸߶� | ||
| Ŀ�� | ������ѧ��ѧ֪ʶ����ѧ�������ʵ������---������˸߶� | ||
| ���� | ����һ | ������ | ������ |
ʾ��ͼ | 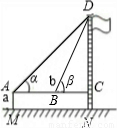 | 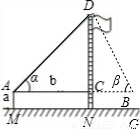 | |
| �������� | Ƥ�ߡ������ | Ƥ�ߡ������ | |
| �������� | AM=1.5m��AB=10m �Ϧ�=30°���Ϧ�=60° | AM=1.5m��AB=20m �Ϧ�=30°���Ϧ�=60° | |
| ������̣��� ���������ţ� | �⣺ | �⣺ | |
��2�����������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д����Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ�����£��á���ʾ��