题目内容
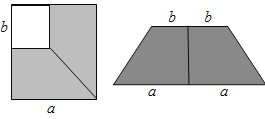
【题目】如图所示，在边长为a的正方形中减去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形如图，分别计算这两个图阴影部分的面积，验证了公式：_____用此公式计算：
_____
【答案】a2b2=(a+b)(ab) 6x
【解析】
根据左图中阴影部分的面积=大正方形的面积-小正方形的面积，或者右图中阴影部分的面积=梯形的面积，由面积不变可得公式．
左图中阴影部分的面积=a2b2，右图中阴影部分的面积=
×(2a+2b)(ab)=(a+b)(ab),由图中阴影部分的面积不变，得a2b2=(a+b)(ab).因此验证的公式为为：a2b2=(a+b)(ab).根据公式计算
（
）
=6x，即答案是a2b2=(a+b)(ab)；6x
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
