Question

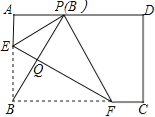
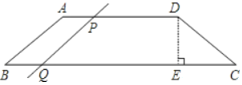
【题目】如图，在四边形ABCD中，AD∥BC，AB=CD，DE⊥BC于点E，且DE=，AD=18，∠C=60°；

（1）BC=________

（2）若动点P从点D出发，速度为2个单位/秒，沿DA向点A运动，同时，动点Q从点B出发，速度为3个单位/秒，沿BC向点C运动，当一个动点到达端点时，另一个动点同时停止运动，设运动的时间为t秒。

①t=_______秒时，四边形PQED是矩形；

②t为何值时，线段PQ与四边形ABCD的边构成平行四边形；

③是否存在t值，使②中的平行四边形是菱形？若存在，请求出t值，若不存在，请说明理由。

Answer 1

【答案】（1）26；（2）①；②当t=或时，，线段PQ与四边形ABCD的边构成平行四边形；③不存在t值，使②中的平行四边形是菱形，理由详见解析.

【解析】

（1）先在Rt△DEC中利用特殊三角函数值可求CE，进而可求CD，再利用等腰梯形的性质可求BC；（2）①先画图，由于四边形PQED是矩形，那么矩形的对边相等，于是PD=QE，再根据路程=速度×时间，可得2t=26-4-3t，进而可求t；②有两种情况：（i）是PQ与AB构成平行四边形，根据平行四边形的性质，对边相等，可得AP=BQ，再根据路程=速度×时间，可得3t=18-2t，进而可求t； （ii）是PQ与CD构成平行四边形，根据平行四边形的性质，对边相等，可得PD=CQ，再根据路程=速度×时间，可得2t=26-3t，进而可求t；③根据②中的两种情况，分别求出BQ、DP的值，再与邻边AB、CD比较，从而可判断不存在t值，使②中的平行四边形是菱形．

∵DE⊥BC，

∴∠DEC=90°，

又∵∠C=60°，

∴CE==4，∠EDC=30°，

∴CD=2CE=8，

∵AD∥BC，AB=CD，

∴四边形ABD是等腰梯形，

∴BC=2CE+AD=8+18=26；

故答案为：26；

（2）①设运动时间为t时，四边形PQED是矩形，如图，

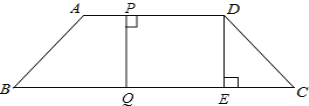
∵四边形PQED是矩形，

∴PD=QE，

∴2t=26-4-3t，

解得t=；

故答案为：；

②有两种情况：

（i）设运动时间为t时，线段PQ与AB构成平行四边形，如图，

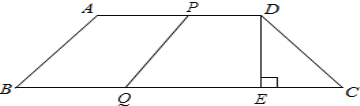
∵四边形ABQP是平行四边形，

∴AP=BQ，

∴3t=18-2t，

解得t=，

（ii）设运动时间为t时，线段PQ与CD构成平行四边形，如图，

∵四边形PQCD是平行四边形，

∴PD=CQ，

∴2t=26-3t，

解得t= ，

综上，当t=或时，，线段PQ与四边形ABCD的边构成平行四边形；

③不存在t值，使②中的平行四边形是菱形，

（i）当t=时，BQ=3t= ，

而AB=CD=8，

所以BQ≠AB，

∴四边形ABQP不是菱形，

（ii）当t=时，DP=2t=，

而AB=CD=8，

所以DP≠AB，

∴四边形PQCD不是菱形．