题目内容
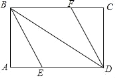
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF为平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
(3)在(2)的条件下,当AE=3时,求四边形BEDF的面积.
【答案】(1)见解析;(2)见解析;(3)18![]() .
.
【解析】
(1)由BE、DF均为角平分线可得∠EBD=∠FDB,则BE∥DF,再由题意可知BF∥DE,故利用两组对边分别平行可证明;
(2)菱形的四边相等,则∠ABE=∠EBD=∠EDB,又由∠ABD+∠EDB=90可求解出∠ABE的度数;
(3)分别求解出AB和ED的长度,利用菱形面积公式计算即可.
证明:(1)∵四边形ABCD是矩形
∴AB∥CD,BC∥AD,∠A=90°=∠ABC
∵AB∥CD
∴∠ABD=∠BDC
∵BE,DF分别平分∠ABD,∠BDC
∴∠ABE=∠DBE=![]() ∠ABD,∠CDF=∠BDF=
∠ABD,∠CDF=∠BDF=![]() ∠BDC
∠BDC
∴∠EBD=∠FDB
∴BE∥DF且AD∥BC
∴四边形BEDF为平行四边形
(2)若四边形BEDF是菱形
∴∠CBD=∠DBE,且∠DBE=∠ABE
∴∠CBD=∠DBE=∠ABE
∵∠CBD+∠DBE+∠ABE=90°
∴∠ABE=30°
∴当∠ABE=30°时,四边形BEDF是菱形
(3)∵∠A=90°,∠ABE=30°,AE=3
∴BE=6,AB=![]() AE=3
AE=3![]()
∵四边形BEDF是菱形
∴BE=DE=6
∴四边形BEDF的面积=DE×AB=18![]()

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目