题目内容
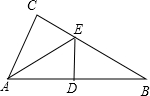
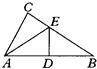9、如图，若D是直角△ABC斜边上的中点，DE⊥AB，如果∠EAC：∠BAE=2：5，那么∠BAC=（ ）分析：由于D是直角△ABC斜边上的中点，DE⊥AB，可以得到AE=BE，进一步得到∠EAB=∠B，又∠EAC：∠BAE=2：5，再利用直角三角形的两个锐角互余即可求出∠BAC．
解答：解：∵D是直角△ABC斜边上的中点，DE⊥AB，
∴AE=BE，
∴∠EAB=∠B，
∵∠EAC：∠BAE=2：5，
∴∠EAC：∠B=2：5，
∴∠BAC：B=7：5，
∵∠BAC+∠B=90°，
∴∠BAC=52°30′，
故选B．
∴AE=BE，
∴∠EAB=∠B，
∵∠EAC：∠BAE=2：5，
∴∠EAC：∠B=2：5，
∴∠BAC：B=7：5，
∵∠BAC+∠B=90°，
∴∠BAC=52°30′，
故选B．
点评：此题考查了直角三角形的性质，还考查了线段垂直平分线的性质，解题时要注意数形结合思想的应用．
练习册系列答案
相关题目
