题目内容
已知,正方形DEFG内接于△ABC中,且点E,F在BC上,点D,G分别在AB,AC上,
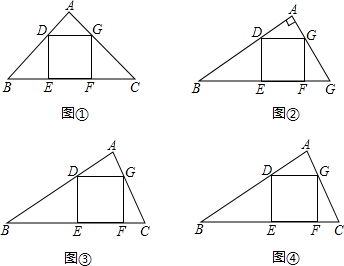
(1)如图①,若△ABC是等腰直角三角形,AB=AC,∠A=90°,S△ADG=2,则S△ABC=
(2)如图②,若△ABC是直角三角形,∠A=90°,AB=4,AC=3,求正方形的边长.
(3)如图③,若△ABC是任意三角形,S△ADG=1,S△BDE=3,S△FCG=1,则正方形的边长为
(4)如图④,若△ABC是任意三角形,求证:S正方形DEFG≤
S△ABC.

(1)如图①,若△ABC是等腰直角三角形,AB=AC,∠A=90°,S△ADG=2,则S△ABC=
18
18
.(2)如图②,若△ABC是直角三角形,∠A=90°,AB=4,AC=3,求正方形的边长.
(3)如图③,若△ABC是任意三角形,S△ADG=1,S△BDE=3,S△FCG=1,则正方形的边长为
2
2
.(4)如图④,若△ABC是任意三角形,求证:S正方形DEFG≤
| 1 | 2 |
分析:(1)设正方形DEFG的边长为x,根据等腰直角三角形的性质BC边上的高等于
BC,然后根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式求出x与BC的比,再根据相似三角形面积的比等于相似比的平方列式计算即可得解;
(2)利用勾股定理列式求出BC,再根据三角形的面积求出BC边上的高,然后根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式计算即可;
(3)设正方形DEFG的边长为x,△ADG边DG上的高为y,根据等底的三角形的面积的比等于高的比用y表示出BE、CF,然后根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式求出x与y的关系,再根据△ADG的面积列式求出x,然后根据正方形的面积列式计算即可得解;
(4)设正方形DEFG的边长为x,△ABC边BC上的高为h,根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式整理得到x,然后放缩不等式得到x,再平方根据正方形的面积和三角形的面积公式即可得证.
| 1 |
| 2 |
(2)利用勾股定理列式求出BC,再根据三角形的面积求出BC边上的高,然后根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式计算即可;
(3)设正方形DEFG的边长为x,△ADG边DG上的高为y,根据等底的三角形的面积的比等于高的比用y表示出BE、CF,然后根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式求出x与y的关系,再根据△ADG的面积列式求出x,然后根据正方形的面积列式计算即可得解;
(4)设正方形DEFG的边长为x,△ABC边BC上的高为h,根据△ADG和△ABC相似,利用相似三角形对应高的比等于对应边的比列式整理得到x,然后放缩不等式得到x,再平方根据正方形的面积和三角形的面积公式即可得证.
解答:解:(1)设正方形DEFG的边长为x,
∵△ABC是等腰直角三角形,AB=AC,
∴BC边上的高等于
BC,
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,
整理得,BC=3x,
∴
=
,
∵△ADG∽△ABC,
∴
=(
)2,
即
=
,
解得S△ABC=18;
(2)∵∠A=90°,AB=4,AC=3,
∴BC=
=
=5,
设△ABC边BC上的高为h,
则S△ABC=
×5h=
×4×3,
解得h=
,
设正方形DEFG的边长为x,
∵DG∥BC,
∴△ADG∽△ABC,
=
,
解得x=
;
(3)设正方形DEFG的边长为x,△ADG边DG上的高为y,
∵S△ADG=1,S△BDE=3,S△FCG=1,
∴BE=3y,CF=y,
∴BC=3y+x+y=x+4y,
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,
整理得,x=2y,
∴S△ADG=
xy=
2y•y=1,
解得y=1,
∴x=2,
即正方形的边长为2;
(4)证明:设正方形DEFG的边长为x,△ABC边BC上的高为h,
∵DG∥BC,
∴△ADG∽△ABC,
∴
=
,
∴x=
=
,
∵
+
≥2
(当且仅当BC=h时取等号),
∴x≤
,
•x2≤
BC•h,
又∵正方形的面积=x2,△ABC的面积=
BC•h,
∴S正方形DEFG≤
S△ABC.
∵△ABC是等腰直角三角形,AB=AC,
∴BC边上的高等于
| 1 |
| 2 |
∵DG∥BC,
∴△ADG∽△ABC,
∴
| ||
|
| x |
| BC |
整理得,BC=3x,
∴
| x |
| BC |
| 1 |
| 3 |
∵△ADG∽△ABC,
∴
| SADG |
| S△ABC |
| x |
| BC |
即
| 2 |
| S△ABC |
| 1 |
| 9 |
解得S△ABC=18;
(2)∵∠A=90°,AB=4,AC=3,
∴BC=
| AB2+AC2 |
| 42+32 |
设△ABC边BC上的高为h,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
解得h=
| 12 |
| 5 |
设正方形DEFG的边长为x,
∵DG∥BC,
∴△ADG∽△ABC,
| ||
|
| x |
| 5 |
解得x=
| 60 |
| 37 |
(3)设正方形DEFG的边长为x,△ADG边DG上的高为y,
∵S△ADG=1,S△BDE=3,S△FCG=1,
∴BE=3y,CF=y,
∴BC=3y+x+y=x+4y,
∵DG∥BC,
∴△ADG∽△ABC,
∴
| y |
| x+y |
| x |
| x+4y |
整理得,x=2y,
∴S△ADG=
| 1 |
| 2 |
| 1 |
| 2 |
解得y=1,
∴x=2,
即正方形的边长为2;
(4)证明:设正方形DEFG的边长为x,△ABC边BC上的高为h,
∵DG∥BC,
∴△ADG∽△ABC,
∴
| h-x |
| h |
| x |
| BC |
∴x=
| BC•h |
| BC+h |
| 1 | ||||
|
∵
| 1 |
| BC |
| 1 |
| h |
|
∴x≤
| ||
| 2 |
•x2≤
| 1 |
| 4 |
又∵正方形的面积=x2,△ABC的面积=
| 1 |
| 2 |
∴S正方形DEFG≤
| 1 |
| 2 |
点评:本题是相似形综合题,主要考查了正方形的性质,相似三角形对应高的比等于相似比的性质,三角形的面积,(3)利用等底的三角形的面积的比等于对应高的比表示出BE、CF是解题的关键,(4)利用不等式放缩用BC、h表示出x是解题的关键.

练习册系列答案
相关题目
 CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离.

