Question

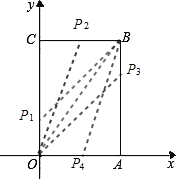
【题目】如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，6），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-C-B-A-O的路线循环移动．

（1）写出点B的坐标；

（2）当点P移动了4秒时，求出此时点P的坐标；

（3）在移动第一周的过程中，当△OBP的面积是8时，求出此时点P的坐标；

（4）若在点P出发的同时，另外有一点Q也从原点出发，以每秒1个单位长度的速度沿着O-A-B-C-O的路线循环运动，请直接写出点P和点Q在第2020次相遇时的坐标．

Answer 1

【答案】（1）点B（4，6）；（2）点P坐标为（2，6）；（3）（0，4），（，6），（4，2），（，0）；（4）（4，）.

【解析】

（1）由矩形的性质可得AB=OC=6，BC=OA=4，可求点B坐标；

（2）由题意可得点P在BC上，即可求点P坐标；

（3）分点P在OC上，在BC上，在AB上，在AO上四种情况讨论，由三角形的面积公式可求点P坐标；

（4）找到点P和点Q相遇时坐标规律可求解．

（1）∵A点的坐标为（4，0），C点的坐标为（0，6），

∴OA=4，OC=6.

∵四边形ABCO是矩形，

∴AB=OC=6，BC=OA=4，

∴点B（4，6）；

（2）∵4×2=8＞6，

∴点P在BC上，

∴PC=2，

∴点P坐标为（2，6）；

（3）如图，

①当点P在OC上时，S△OBP==8，

∴OP1=4，

∴点P（0，4），

②当点P在BC上，S△OBP=BP2×6=8，

∴BP2=，

∴CP2=4-=，

∴点P（，6），

③当点P在AB上，S△OBP=BP3×4=8，

∴BP3=4，

∴AP3=2，

∴点P（4，2），

④当点P在AO上，S△OBP=OP4×6=8，

∴OP4=，

∴点P（，0），

（3）∵第一次相遇所需时间==s，

∴点P，点Q相遇时坐标为（4，），

同理可求：第二次相遇时坐标为（，6），第三次相遇时坐标为（0，0），第四次相遇时坐标为（4，），

∵2020÷3=673…1，

∴点P和点Q在第2020次相遇时的坐标为（4，）.