题目内容
【题目】一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上. 
(1)若设AE=x,则AF=;(用含x的代数式表示)
(2)要使剪出的矩形CDEF的面积最大,点E应选在何处?
【答案】
(1)![]() x
x
(2)解:∵四边形CDEF是矩形,
∴∠AFE=90°,
∵∠A=30°,
∴EF= ![]() AE=
AE= ![]() x,
x,
在Rt△ABC中,∠C=90°,AB=12,
∴BC= ![]() AB=6,
AB=6,
根据勾股定理得:AC= ![]() =6
=6 ![]() ,
,
∴CF=AC﹣AF=6 ![]() ﹣
﹣ ![]() x,
x,
∴S矩形CDEF=CFEF= ![]() x(6
x(6 ![]() ﹣
﹣ ![]() x)=﹣
x)=﹣ ![]() (x﹣6)2+9
(x﹣6)2+9 ![]() ,
,
∴当x=6时,矩形CDEF的面积最大,
即当点E为AB的中点时,矩形CDEF的面积最大.
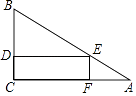
【解析】解:(1)在Rt△ABC中,∠A=30°,∠C=90°,AE=x, ∴EF= ![]() x,根据勾股定理得:AF=
x,根据勾股定理得:AF= ![]() x;所以答案是:
x;所以答案是: ![]() x;
x;
【考点精析】根据题目的已知条件,利用二次函数的最值和矩形的性质的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目

