题目内容
【题目】如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,
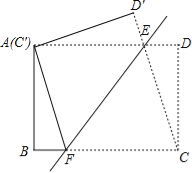
(1)求证:四边形AFCE为菱形;
(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
【答案】(1)证明见解析,(2)a2=b2+c2.
【解析】试题分析:(1)由矩形ABCD与折叠的性质,易证得△CEF是等腰三角形,即CE=CF,即可证得AF=CF=CE=AE,即可得四边形AFCE为菱形;
(2)由折叠的性质,可得CE=AE=a,在Rt△DCE中,利用勾股定理即可求得:a、b、c三者之间的数量关系式为:a2=b2+c2.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF=∠EFC,
由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,
∴∠EFC=∠CEF,
∴CF=CE,
∴AF=CF=CE=AE,
∴四边形AFCE为菱形;
(2)a、b、c三者之间的数量关系式为:a2=b2+c2.
理由:由折叠的性质,得:CE=AE,
∵四边形ABCD是矩形,
∴∠D=90°,
∵AE=a,ED=b,DC=c,
∴CE=AE=a,
在Rt△DCE中,CE2=CD2+DE2,
∴a、b、c三者之间的数量关系式为:a2=b2+c2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目