题目内容
【题目】已知：在Rt△ABC，∠ABC=90°，∠C=60°，现将一个足够大的直角三角板的顶点P放在斜边AC上．
（1）设三角板的两直角边分别交边AB、BC于点M、N．
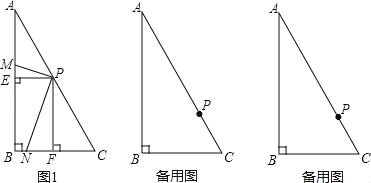
①当点P是AC的中点时，分别作PE⊥AB于点E，PF⊥BC于点F，得到图1，写出图中的一对全等三角形；
②在①的条件下，写出与△PEM相似的三角形，并直接写出PN与PM的数量关系．
（2）移动点P，使AP=2CP，将三角板绕点P旋转，设旋转过程中三角板的两直角边分别交边AB、BC于点M、N（PM不与边AB垂直，PN不与边BC垂直）；或者三角板的两直角边分别交边AB、BC的延长线与点M、N．
③请在备用图中画出图形，判断PM与PN的数量关系，并选择其中一种图形证明你的结论；
④在③的条件下，当△PCN是等腰三角形时，若BC=3cm，则线段BN的长是 ．
【答案】(1)、①△AEP≌△PFC；理由见解析；②、△PFN∽△PEM，PN=
PM；理由见解析；(2)、③、答案见解析；④、1cm或5cm
【解析】
试题分析：(1)、①求出∠AEP=∠B=∠PFC=90°，∠APE=∠C=60°，根据AAS推出两三角形全等即可；②求出AB=
BC，求出PE=
BC，PF=
AB，推出
，求出∠EPM=∠NPF=90°﹣∠MPF，∠PEM=∠PFN=90°，根据相似三角形的判定推出△PFN∽△PEM，推出
，即可得出答案；(2)、③过P作PE⊥AB于E，PF⊥BC于F，求出△AEP∽∠PFC，推出
=2，设CF=x，则PE=2x，求出PF=x，证△PEM∽△PFN，推出
即可；④求出CP=2cm，分为两种情况：第一种情况：当N在线段BC上时，得出△PCN是等边三角形，求出CN=CP=2cm，代入BN=BC﹣CN求出即可；第二种情况：当N在线段BC的延长线上时，求出CN=PC=2cm，代入BN=BC+CN求出即可．
试题解析：(1)、①△AEP≌△PFC，
理由是：∵P为AC中点，∴AP=PC，∵PE⊥AB，PF⊥BC，∠B=90°，∴∠AEP=∠B=∠PFC=90°，
∴PF∥AB，PE∥BC，∴∠APE=∠C=60°，在△AEP和△PFC中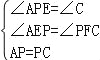
∴△AEP≌△PFC（AAS）．
②、△PFN∽△PEM，PN=PM，
理由是：∵在Rt△ACB中，∠ABC=90°，∠C=60°，∴AB=BC，
∵PE∥BC，PF∥AB，P为AC中点，∴E为AB中点，F为BC中点，∴PE=BC，PF=AB，
∴
，∵∠PEB=∠B=∠PFB=90°，∴∠EPF=90°，∵∠MPN=90°，
∴∠EPM=∠NPF=90°﹣∠MPF，∵∠PEM=∠PFN=90°，∴△PFN∽△PEM，∴
，∴PN=PM．
(2)、③PM=2PN，如图，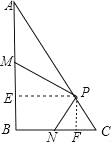
过P作PE⊥AB于E，PF⊥BC于F，∵∠AEP=∠PFC=∠B=90°，∴PE∥BC，∴∠APE=∠C，
∴△AEP∽∠PFC，∴
=
=
=2，设CF=x，则PE=2x，在Rt△PFC中，∠C=60°，∠PFC=90°，
∴PF=x，∵在四边形BFPE中，∠BFP=∠B=∠BEP=90°，∴∠EPF=90°，即∠EPM+∠MPF=90°，
∵∠NPF+∠MPF=90°，∴∠NPF=∠EPM，∵∠MEP=∠PFN=90°，∴△PEM∽△PFN，
∴
=
=
=
，∴PM=PN．
④、∵在Rt△ABC中，∠B=90°，∠C=60°，BC=3cm ∴AC=2BC=6cm，∵AP=2PC，∴CP=2cm，
分为两种情况：第一种情况：当N在线段BC上时，如图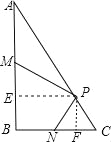
∵△PCN是等腰三角形，∠C=60°，CP=2cm，∴△PCN是等边三角形，∴CN=CP=2cm，
∴BN=BC﹣CN=3cm﹣2cm=1cm；
第二种情况：当N在线段BC的延长线上时，如图，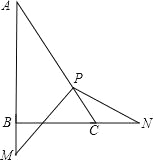
∵∠PCN=180°﹣60°=120°，∴要△PCN是等腰三角形，只能PC=CN，即CN=PC=2cm，
∴BN=BC+CN=3cm+2cm=5cm，即BN的长是1cm或5cm，
