Question

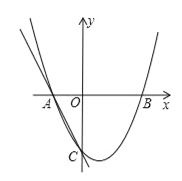
【题目】如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．

（1）求二次函数的解析式；

（2）点P在x轴正半轴上，且PA=PC，求OP的长；

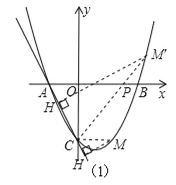
（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．

①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；

②若⊙M的半径为，求点M的坐标．

Answer 1

【答案】(1) y=x2﹣x﹣2 (2) OP= (3) ①M（1，﹣2） M′（， ）

②点M的坐标为（ ，3+）或（，3﹣）

【解析】试题分析: （1）根据与x轴的两个交点A、B的坐标，设出二次函数交点式解析式y=a（x+1）（x﹣2），然后把点C的坐标代入计算求出a的值，即可得到二次函数解析式；

（2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可；

（3）①根据相似三角形对应角相等可得∠MCH=∠CAO，然后分（i）点H在点C下方时，利用同位角相等，两直线平行判定CM∥x轴，从而得到点M的纵坐标与点C的纵坐标相同，是﹣2，代入抛物线解析式计算即可；（ii）点H在点C上方时，根据（2）的结论，点M为直线PC与抛物线的另一交点，求出直线PC的解析式，与抛物线的解析式联立求解即可得到点M的坐标；

②在x轴上取一点D，过点D作DE⊥AC于点E，可以证明△AED和△AOC相似，根据相似三角形对应边成比例列式求解即可得到AD的长度，然后分点D在点A的左边与右边两种情况求出OD的长度，从而得到点D的坐标，再作直线DM∥AC，然后求出直线DM的解析式，与抛物线解析式联立求解即可得到点M的坐标．

试题解析:

（1）设该二次函数的解析式为：y=a（x+1）（x﹣2），

将x=0，y=﹣2代入，得﹣2=a（0+1）（0﹣2），

解得a=1，

∴抛物线的解析式为y=（x+1）（x﹣2），

即y=x2﹣x﹣2；

（2）设OP=x，则PC=PA=x+1，

在Rt△POC中，由勾股定理，得x2+22=（x+1）2，

解得，x=，

即OP=；

（3）①∵△CHM∽△AOC，

∴∠MCH=∠CAO，

（i）如图1，当H在点C下方时，

∵∠OAC+∠OCA=90°，∠MCH=∠OAC

∴∠OCA+∠MCH=90°

∴∠OCM=90°=∠AOC

∴CM∥x轴

∴yM=﹣2，

∴x2﹣x﹣2=﹣2，

解得x1=0（舍去），x2=1，

∴M（1，﹣2），

（ii）如图1，当H在点C上方时，

∵∠MCH=∠CAO，

∴PA=PC，由（2）得，M′为直线CP与抛物线的另一交点，

设直线CM′的解析式为y=kx﹣2，

把P（，0）的坐标代入，得k﹣2=0，

解得k=，

∴y=x﹣2，

由x﹣2=x2﹣x﹣2，

解得x1=0（舍去），x2=，

此时y=×﹣2=，

∴M′（， ），

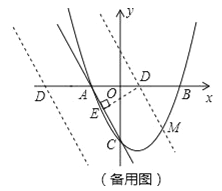
②在x轴上取一点D，如图（备用图），过点D作DE⊥AC于点E，使DE= ，

在Rt△AOC中，AC===，

∵∠COA=∠DEA=90°，∠OAC=∠EAD，

∴△AED∽△AOC，

∴ =，

即= ，

解得AD=2，

∴D（1，0）或D（﹣3，0）．

过点D作DM∥AC，交抛物线于M，如图（备用图）

则直线DM的解析式为：y=﹣2x+2或y=﹣2x﹣6，

当﹣2x﹣6=x2﹣x﹣2时，即x2+x+4=0，方程无实数根，

当﹣2x+2=x2﹣x﹣2时，即x2+x﹣4=0，解得x1=，x2=，

∴点M的坐标为（ ，3+）或（，3﹣）．