题目内容
如图,矩形OABC的顶点B的坐标为(1,2),反比例函数y= (0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.
(0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.
(1)若点E是AB的中点,则m= ,S△OEF= ;
(2)若S△OEF=2S△BEF,求点E的坐标;
(3)是否存在点E及y轴上的点M,使得△MFE与△BFE全等?若存在,写出此时点E的坐标;若不存在,说明理由.
(1)m=1;S△OEF= ;
;
(2)点E的坐标为(1, )
)
(3)存在;E点坐标为(1, )
)
解析试题分析:(1)先得到E点坐标为(1,1),然后根据反比例函数图象上点的坐标特征即可得到k=1,再利用F的纵坐标为2可确定F点坐标为(  ,2),则可根据S△OEF=S矩形ABCO-S△AOE-S△OCF-S△BEF进行计算;
,2),则可根据S△OEF=S矩形ABCO-S△AOE-S△OCF-S△BEF进行计算;
(2)由题意,E(1,m),F( ,2),可表示出△BEF的面积,进而可表示出△OEF与△BEF的面积之和,从而可得到m的值,进而得到点E的坐标;
,2),可表示出△BEF的面积,进而可表示出△OEF与△BEF的面积之和,从而可得到m的值,进而得到点E的坐标;
作EH⊥y轴于C,如图,设E点坐标为(1,m),则F( ,2),:
,2),:
由于m<2,则由△MFE≌△BFE得到MF="BF=1-m"
ME=BE=2-m,∠FME=90°,易证得Rt△CFM∽Rt△HME,利用相似比可得到MH=m,然后在Rt△MHM中,根据勾股定理得12+m2=(2-km)2,解得m= ,则E点坐标为(1,
,则E点坐标为(1, )
)
试题解析:(1)∵B点坐标为(1,2),点E是AB的中点,AB⊥X轴,
∴E点坐标为(1,1),
∵点E在函数为y= 上,
上,
∴1= ,
,
∴m=1
把y=2代入y= 得
得 =2,解得x=
=2,解得x= ,
,
∴F点坐标为( ,2),
,2),
∴S△OEF=S矩形ABCO-S△AOE-S△OCF-S△BEF
=1×2- ×1×1 -
×1×1 - ×
× ×2-
×2- ×
× × 1
× 1
= ;
;
(2)根据题意,E(1,m),F( ,2)
,2)
∴S△BEF= ,
,
∵S△OAE=S△OCF=
∴S△BEF+S△OEF=2-m,
∵S△OEF=2S△BEF,
∴S△BEF= ,
,
∴ =
= ,
,
解得,m=2(舍去),或m=
∴点E的坐标为(1, )
)
(3)作EH⊥y轴于C,如图,
设E点坐标为(1,m),则F( ,2),
,2),
当m<2时,
∵△MFE≌△BFE,
∴MF=BF=1- ,ME=BE=2-m,∠FME=90°,
,ME=BE=2-m,∠FME=90°,
∴Rt△CFM∽Rt△HME,
∴MF:ME=CF:MH,
∴MH= =m,
=m,
在Rt△MHM中,HE=1,
∴HE2+MH2=ME2,
∴12+m2=(2-m)2,解得m= ,
,
∴E点坐标为(1, )
)
考点:1、反比例函数图象上点的坐标特征;2、三角形全等的性质和矩形性质;3、勾股定理;4、相似比

 的图象上,第二象限内的点B在反比例函数
的图象上,第二象限内的点B在反比例函数 的图象上,连接OA、OB,若OA⊥OB,OB=
的图象上,连接OA、OB,若OA⊥OB,OB= OA,则k= .
OA,则k= . 位于第一象限的图象上,则k的值为 .
位于第一象限的图象上,则k的值为 .
 的图象经过点(1,2),则k= 。
的图象经过点(1,2),则k= 。 的图象的一支.根据给出的图象回答下列问题:
的图象的一支.根据给出的图象回答下列问题:
 、
、 分别与双曲线
分别与双曲线 相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1). 值及
值及 点坐标;(4分)
点坐标;(4分) ,求P点坐标.(4分)
,求P点坐标.(4分)
 的坐标为(
的坐标为( ,
,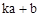 )(其中k为常数,且
)(其中k为常数,且 ),则称点
),则称点 ,
, ),即
),即 的“2属派生点”
的“2属派生点”  为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________; ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.
 的图象,并根据图象回答问题.
的图象,并根据图象回答问题.