题目内容
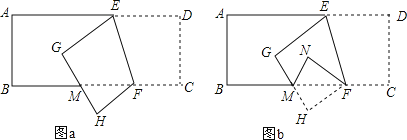
【题目】如图a,已知长方形纸带ABCD,AB∥CD,AD∥BC,∠BFE=70°,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b.
(1)图a中,∠AEG=______°;
(2)图a中,∠BMG=______°;
(3)图b中,∠EFN=______°.
【答案】(1)40°;(2)50°;(3)30°.
【解析】
(1)根据平行线的性质求出∠DEF的度数,由折叠的性质和平角的定义即可得出结论;
(2)由(1)知,∠HFM=40°,再由翻折变换的性质得出∠H=∠C=90°,由三角形内角和定理得出∠HMF的度数,根据对顶角相等即可得出结论;
(3)先根据图形翻折变换的性质得出∠MFN=∠HFM=40°,再由∠BFE=70°即可得出结论.
(1)∵∠BFE=70°,AD∥BC,
∴∠DEF=∠BFE=70°,
∴∠GEF=∠DEF=70°,
∴∠AEG=180°-70°-70°=40°.

(2)∵由(1)知,∠HFM=40°,∠H=∠C=90°,
∴∠HMF=90°-40°=50°.
∵∠HMF与∠BMG是对顶角,
∴∠BMG=∠HMF=50°.
(3)∵△MNF由△MHF翻折而成,
∴∠MFN=∠HFM=40°,
∵∠BFE=70°,
∴∠EFN=∠BFE-∠MFN=70°-40°=30°.

练习册系列答案
相关题目