题目内容
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
【答案】(1)B;(2)![]() 的最小整数解为
的最小整数解为![]() ;(3)隐线中
;(3)隐线中![]() 的最大值和最小值的和为
的最大值和最小值的和为![]()
【解析】
(1)将A,B,C三点坐标代入方程,方程成立的点即为所求,
(2)将P,Q代入方程,组成方程组求解即可,
(3)将P代入隐线方程,与![]() 组成方程组,求解方程组的解,再由
组成方程组,求解方程组的解,再由![]() 即可求解.
即可求解.
解:(1)将A,B,C三点坐标代入方程,只有B点符合,
∴隐线![]() 的亮点的是B.
的亮点的是B.
(2)将![]() 代入隐线方程
代入隐线方程
得: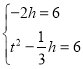
解得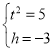
代入方程得:![]()
![]() 的最小整数解为
的最小整数解为![]()
(3)由题意可得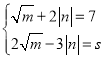
![]()
![]()
![]()
![]()
![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]()
隐线中![]() 的最大值和最小值的和为
的最大值和最小值的和为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目