题目内容
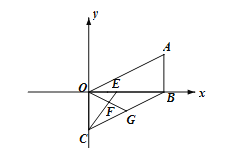
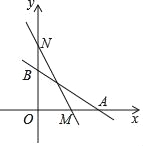
【题目】如图,直线:y=﹣![]() x+b与x轴分别交于A(4,0)、B两点,在y轴上有一点N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动.
x+b与x轴分别交于A(4,0)、B两点,在y轴上有一点N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动.
(1)点B的坐标为 ;
(2)求△MNO的面积S与移动时间t之间的函数关系式;
(3)当t= 时,△NOM≌△AOB;
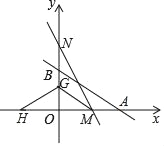
(4)若M在x轴正半轴上,且△NOM≌△AOB,G是线段ON上一点,连结MG,将△MGN沿MG折叠,点N恰好落在x轴上的H处,求G点的坐标.
【答案】(1)(0,2)(2)S=|8﹣2t|(3)2或6(4)(0,![]() ﹣1)
﹣1)
【解析】
(1)由点A的坐标利用待定系数法可求出b值,再利用一次函数图象上点的坐标特征可求出点B的坐标;
(2)由点A、H的坐标及点M移动的速度可得出ON、OM的长度,再利用三角形的面积公式即可找出△MNO的面积S与移动时间t之间的函数关系式;
(3)由OA=ON=4、∠AOB=∠NOM=90°,可得出若要△NOM≌△AOB只需OM=OB=2,结合OM=|4﹣t|可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(4)设点G的坐标为(0,y),则OG=y,由折叠的性质可找出GH、OH的长度,在Rt△GOH中,利用勾股定理可得出关于y的一元一次方程,解之即可得出结论.
(1)∵直线y=﹣![]() x+b过点A(4,0),
x+b过点A(4,0),
∴0=﹣![]() ×4+b,解得:b=2,
×4+b,解得:b=2,
∴直线AB的函数关系式为y=﹣![]() x+2.
x+2.
当x=0时,y=﹣![]() x+2=2,
x+2=2,
∴点B的坐标为(0,2).
故答案为:(0,2).
(2)∵A(4,0),N(0,4),动点M从点A以每秒1个单位的速度匀速沿x轴向左移动,
∴OA=4,ON=4,OM=OA﹣AM=|4﹣t|,
∴S=![]() OMON=
OMON=![]() |4﹣t|×4=|8﹣2t|.
|4﹣t|×4=|8﹣2t|.
(3)∵OA=ON=4,∠AOB=∠NOM=90°,
∴若要△NOM≌△AOB,只需OM=OB=2.
∵OM=|4﹣t|,
∴|4﹣t|=2,
解得:t=2或6.
故答案为:2或6.
(4)设点G的坐标为(0,y),则OG=y.
根据折叠的性质,可知:MH=MN=![]() =2
=2![]() ,GH=GN=4﹣y,
,GH=GN=4﹣y,
∴OH=2![]() ﹣2.
﹣2.
在Rt△GOH中,GH2=OG2+OH2,即(4﹣y)2=y2+(2![]() ﹣2)2,
﹣2)2,
解得:y=![]() ﹣1,
﹣1,
∴点G的坐标为(0,![]() ﹣1).
﹣1).

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?