Question

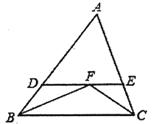
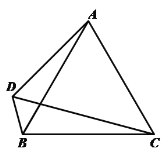
【题目】如图，在等边△中，作，边CD、BD交于点D，连接AD.

（1）请直接写出的度数；

（2）求的度数；

（3）用等式表示线段AC、BD、CD三者之间的数量关系，并证明．

Answer 1

【答案】（1）60°；（2）；（3）.证明见解析.

【解析】

（1）设AB与CD的交点为O，有，，根据三角形内角和定理可得:==60°；

（2）有两角相等得△AOC∽△DOB，所以，且夹角相等，再得△AOD∽△COB，从而求得.

（3）现由SAS证明△ADE≌△ADB，再证明是等腰直角三角形即可解答.

（1）；

（2）设AB与CD的交点为O.

∵，，

∴△AOC∽△DOB.

∴.

∵，

∴△AOD∽△COB.

∴.

（3）答案一：线段AC、BD、CD三者之间的数量关系为.

证明：如图，延长CD到点E，使，连接AE.

∵，

∴.

∵，

∴.

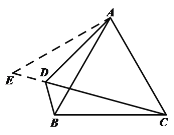
在△ADE和△ADB中，

∴△ADE≌△ADB.

∴，.

∵，

∴，.

∴.

∴.

另一种证法：延长BD到点E，使，连接AE.

答案二：线段AC、BD、CD三者之间的数量关系为.

证明：如图，在D C上截取，连接BE，过点A作AF⊥CD于点F.

可证△ADB≌△CEB，可得，

，.

，.

，.