题目内容
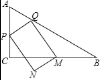
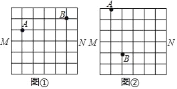
【题目】图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图①、图②给定的网格中按要求作图.
(1)在图①中的格线MN上确定一点P,使PA与PB的长度之和最小
(2)在图②中的格线MN上确定一点Q,使∠AQM=∠BQM.
要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
【答案】(1)见解析;(2)见解析.
【解析】
![]() 如图
如图![]() ,作A关于MN的对称点
,作A关于MN的对称点![]() ,连接
,连接![]() ,交MN于P,P点即为所求;
,交MN于P,P点即为所求;![]() 如图
如图![]() ,作B关于MN的对称点
,作B关于MN的对称点![]() ,连接
,连接![]() 并延长交MN于Q,Q点即为所求.
并延长交MN于Q,Q点即为所求.
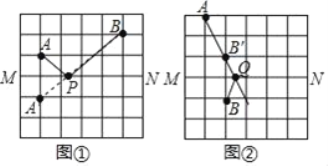
解:(1)如图①,作A关于MN的对称点A′,连接BA′,交MN于P,此时PA+PB=PA′+PB=BA′,根据两点之间线段最短,此时PA+PB最小;
(2)如图②,作B关于MN的对称点B′,连接AB′并延长交MN于Q,此时∠AQM=∠BQM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分 数 段 | 频数 | 频率 |
60≤x<70 | 9 | a |
70≤x<80 | 36 | 0.4 |
80≤x<90 | 27 | b |
90≤x≤100 | c | 0.2 |
请根据上述统计图表,解答下列问题:
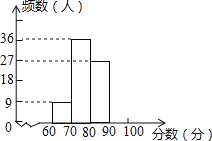
(1)在表中,a= ,b= ,c= ;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?