Question

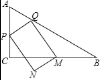
【题目】如阁，在△ABC中，∠ACB＝90°，AC＝3，BC＝4，点P从点A出发，沿折线AC﹣BC以每秒1个单位长度的速度向终点B运动，当点P不与点A、B重合时，在边AB上取一点Q，满足∠PQA＝2∠B，过点Q作QM⊥PQ，交边BC于点M，以PQ、QM为边作矩形PQMN，设点P的运动时间为t秒

（1）用含t的代数式表示线段PQ的长；

（2）当矩形PQMN为正方形时，求t的值；

（3）设矩形PQMN与△ABC重叠部分图形的周长为l，求l与t之间的函数关系式；

（4）作点A关于直线PQ的对称点A′，作点C关于直线PN的对称点C′，当点A′、C′这两个点中只有一个点在矩形PQMN内部时，直接写出此时的t取值范围．

Answer 1

【答案】（1）或；（2）；（3）当时，重叠部分是四边形PQMN，四边形PQMN的周长．当时，重叠部分是，的周长．（4）或.

【解析】

分两种情形分别求解即可解决问题．
如图1中，当四边形PQMN是正方形时，作于利用全等三角形的性质，构建方程即可解决问题如图2中，四边形PQMN不可能是正方形．
分两种情形分别画出图象解决问题即可．
如图5中，当点在线段MQ上时，作于求出t的值如图6中，当点在MN上时，作于求出t的值，由此即可判定．

解：如图1中当时，作于H．

，
，
，
，
，，
≌，
，，
在中，，，
，
，
，
，
，
如图2中，当时，作，

，
，
，
，
，
，
，
，
，
．

如图1中，当四边形PQMN是正方形时，作于K．
，
，
，，
≌，
，
，
，
如图2中，四边形PQMN不可能是正方形，
综上所述，时，四边形PQMN是正方形．

如图3中，当时，重叠部分是四边形PQMT．

由可知：，，，
由∽，可得，
，
，
由∽，
，
，
，
由∽，
，
，
，
四边形PQMN的周长．
如图4中，当时，重叠部分是，

由可知：，，，
的周长．

如图5中，当点在线段MQ上时，作于K．

由可得：，
解得，
观察图象可知：当时，点这两个点中只有一个点在矩形PQMN内部．

如图6中，当点在MN上时，作于K．

由可得：，
解得，
观察图象可知：时，点这两个点中只有一个点在矩形PQMN内部．
综上所述，满足条件的t的值为或．