Question

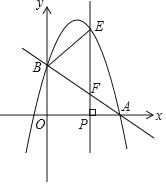
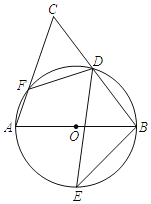
【题目】如图，AB是⊙O的直径，D，E为⊙O上位于AB异侧的两点，连结BD并延长至点C，使得CD＝BD，连结AC交⊙O于点F，连接BE，DE，DF．

（1）若∠E＝35°，求∠BDF的度数．

（2）若DF＝4，cos∠CFD＝，E是的中点，求DE的长．

Answer 1

【答案】（1）∠BDF＝110°；（2）DE＝2+．

【解析】

（1）连接EF，BF，由AB是⊙O的直径，得到∠AFB=∠BFC=90°，推出，得到∠DEF=∠BED=35°，根据圆内接四边形的性质即可得到结论；

（2）连接AD，OE，过B作BG⊥DE于G，解直角三角形得到AB=6，由E是的中点，AB是⊙O的直径，得到∠AOE=90°，根据勾股定理即可得到结论．

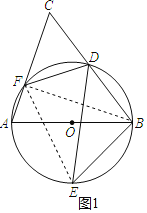
（1）如图1，连接EF，BF，

∵AB是⊙O的直径，

∴∠AFB＝∠BFC＝90°，

∵CD＝BD，

∴DF＝BD＝CD，

∴，

∴∠DEF＝∠BED＝35°，

∴∠BEF＝70°，

∴∠BDF＝180°﹣∠BEF＝110°；

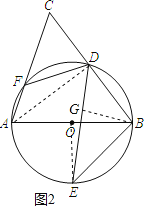
（2）如图2，连接AD，OE，过B作BG⊥DE于G，

∵∠CFD＝∠ABD，

∴cos∠ABD＝cos∠CFD＝，

在Rt△ABD中，BD＝DF＝4，

∴AB＝6，

∵E是的中点，AB是⊙O的直径，

∴∠AOE＝90°，

∵BO＝OE＝3，

∴BE＝3，

∴∠BDE＝∠ADE＝45°，

∴DG＝BG＝BD＝2，

∴GE＝＝，

∴DE＝DG+GE＝2+．