题目内容
已知关于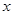 的方程
的方程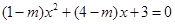 .
.
1.若方程有两个不相等的实数根,求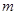 的取值范围;
的取值范围;
2. 若正整数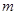 满足
满足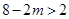 ,设二次函数
,设二次函数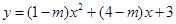 的图象与
的图象与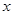 轴交于
轴交于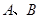 两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线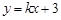 与此图象恰好有三个公共点时,求出
与此图象恰好有三个公共点时,求出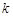 的值(只需要求出两个满足题意的k值即可).
的值(只需要求出两个满足题意的k值即可).
【答案】
1.
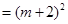 .
.
由题意得, >0且
>0且 .
.
∴ 符合题意的m的取值范围是 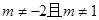 的 一切实数.
的 一切实数.
2.∵ 正整数 满足
满足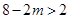 ,
,
∴ m可取的值为1和2 .
又∵ 二次函数 ,
,
∴  =2.
=2.
∴ 二次函数为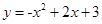 .
.
∴ A点、B点的坐标分别为(-1,0)、(3,0).
依题意翻折后的图象如图所示.
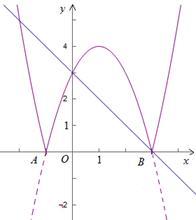
由图象可知符合题意的直线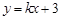 经过点A、B.
经过点A、B.
可求出此时k的值分别为3或-1.
注:若学生利用直线与抛物线相切求出k=2也是符合题意的答案.
【解析】
1.利用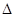 >0和二次项系数不为0计算出m的取值范围;
>0和二次项系数不为0计算出m的取值范围;
2.利用已知求出m的值,得出二次函数的解析式,从而得出A、B两点的坐标,然后翻折得出k的值。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
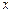 的方程
的方程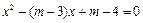 .
.
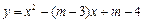 与
与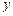 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线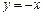 的对称点恰好是点M,求
的对称点恰好是点M,求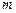 的值.
的值.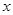 的方程
的方程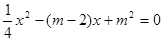
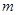 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)