题目内容
 如图,将边长为
如图,将边长为| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
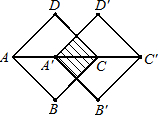
分析:根据题意可得,阴影部分的图形是正方形,正方形ABCD的边长为
,则AC=2,可得出A′C=1,可得出其面积.
| 2 |
解答:解:∵正方形ABCD的边长为
,
∴AC=2,
又∵点A′是线段AC的中点,
∴A′C=1,
∴S阴影=
×1×1=
.
故选B.
| 2 |
∴AC=2,
又∵点A′是线段AC的中点,
∴A′C=1,
∴S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了正方形的性质及平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
相关题目
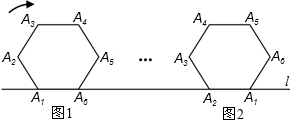
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
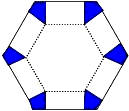 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为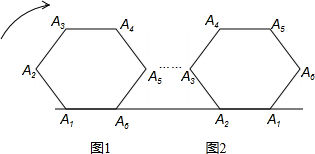 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为