题目内容
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
【答案】
(1)解:如图所示:
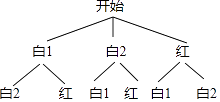
(2)解:共有6种情况,两次摸到的球的颜色不同的情况有4种,概率为 ![]() =
= ![]() .
.
【解析】(1)事件分为几个步骤,树状图就分几层,本题事件分为两个步骤,树状图就分两层;(2)概率P=关注的结果数![]() 机会均等的结果数,两次颜色不同的情况有4种(白红,白红,红白,红白),概率即可求出.
机会均等的结果数,两次颜色不同的情况有4种(白红,白红,红白,红白),概率即可求出.
【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目