Question

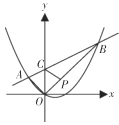
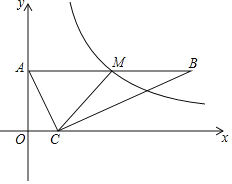
【题目】如图，在平面直角坐标系中，点C、A分别在x轴、y轴上，AB∥x轴，∠ACB＝90°，反比例函数y＝（x＞0）的图象经过AB的中点M．若点A（0，4）、C（2，0），则k的值为（　　）

A.16B.20C.32D.40

Answer 1

【答案】B

【解析】

过点B作BD⊥x轴于点D，证明△AOC∽△CDB，求得CD，得出M点坐标，便可求得结果．

过点B作BD⊥x轴于点D，如图，

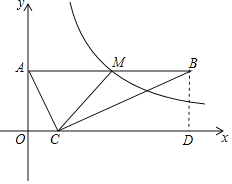
∵AB∥x轴，A（0，4），C（2，0），

∴OA＝BD＝4，OC＝2，

∵∠AOC＝∠ACB＝90°，

∴∠OAC+∠OCA＝∠OCA+∠DCB＝90°，

∴∠OAC＝∠DCB，

∵∠AOC＝∠CDB＝90°，

∴△AOC∽△CDB，

∴，即，

∴DC＝8，

∴AB＝OD＝2+8＝10，

∵M是AB的中点，

∴AM＝5，

∴M（5，4），

∵反比例函数y＝（x＞0）的图象经过AB的中点M，

∴k＝5×4＝20．

故选：B．