题目内容
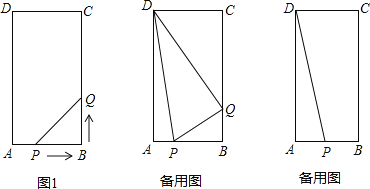
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
【答案】(1)t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2;
(2)△DPQ为直角三角形;
(3)运动开始后第6![]() ﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.
﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.
【解析】试题分析:(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;(2)表示出DP2=![]() ,PQ2=
,PQ2=![]() ,DQ2=117,进而得到PQ2+DQ2=DP2,得出答案;(3)假设运动开始后第x秒时,满足条件,则有QP=QD,表示出QP2,QD2,列出等式,整理得到方程,求出方程的解,根据时间大于0秒小于6秒,即可解答.
,DQ2=117,进而得到PQ2+DQ2=DP2,得出答案;(3)假设运动开始后第x秒时,满足条件,则有QP=QD,表示出QP2,QD2,列出等式,整理得到方程,求出方程的解,根据时间大于0秒小于6秒,即可解答.
试题解析:(1)设经过t秒,△PBQ的面积等于8cm2,
则:BP=6﹣t,BQ=2t,
所以![]() ×(6﹣t)×2t=8,即t2﹣6t+8=0,
×(6﹣t)×2t=8,即t2﹣6t+8=0,
可得:t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2.
(2)当t=![]() 秒时,
秒时,
AP=![]() ,BP=6﹣
,BP=6﹣![]() =
=![]() ,BQ=
,BQ=![]() ×2=3,CQ=12﹣3=9,
×2=3,CQ=12﹣3=9,
∴在Rt△DAP中,![]() ,
,
在Rt△DCQ中,DQ2=DC2+CQ2=62+92=117,
在Rt△QBP中,![]() ,
,
∴![]() ,
,
∴DQ2+QP2=DP2,
∴△DPQ为直角三角形;
(3)假设运动开始后第x秒时,满足条件,则:QP=QD,
∵OP2=PB2+BQ2=(6﹣x)2+(2x)2,
QD2=QC2+CD2=(12﹣2x)2+62,
∴(12﹣2x)2+62=(6﹣x)2+(2x)2,
整理,得:x2+36x﹣144=0,
解得:x=﹣18±6![]() ,
,
∵0<6![]() ﹣18<6,
﹣18<6,
∴运动开始后第6![]() ﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.
﹣18秒时,以Q为圆心,PQ为半径的圆正好经过点D.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
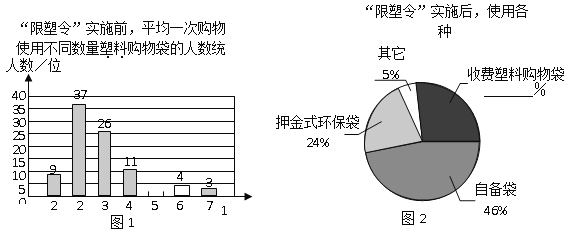
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 总人数的百分比 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
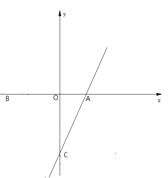
【题目】如图,二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() ,交
,交![]() 轴于点
轴于点![]() ,连接直线
,连接直线![]() .
.
(1)求二次函数的解析式;
(2)点![]() 在二次函数的图像上,圆
在二次函数的图像上,圆![]() 与直线
与直线![]() 相切,切点为
相切,切点为![]() .
.
①若![]() 在
在![]() 轴的左侧,且△
轴的左侧,且△![]() ∽△
∽△![]() ,求点
,求点![]() 的坐标;
的坐标;
②若圆![]() 的半径为4,求点
的半径为4,求点![]() 的坐标.
的坐标.
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
