��Ŀ����
����Ŀ����Rt��ABC�У���C=90�㣬AB=10��AC=8����Q��AB�ϣ���AQ=2����Q��QR��AB������ΪQ��QR������AC��CB��R����ͼ1��������Q��ÿ��2����λ���յ�B�ƶ�ʱ����Pͬʱ��A��������ÿ��6����λ���ٶ���AB��BC��CA�ƶ������ƶ�ʱ��Ϊt�루��ͼ2����
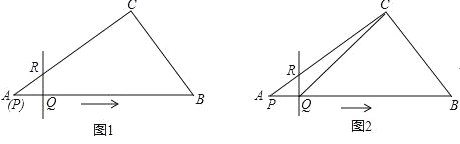
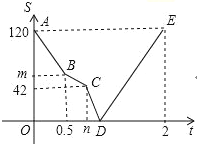
��1�����BCQ�����S��t�ĺ�����ϵʽ��
��2��tΪ��ֵʱ��QP��AC��
��3��tΪ��ֵʱ��ֱ��QR������P��
��4������P��AB���˶�ʱ����PQΪ����AB�Ϸ�������������PQMN��Rt��ABC�ڲ������ʱt��ȡֵ��Χ��
���𰸡���1��S��BCQ=��![]() t+
t+![]() ��0��t��8������2��
��0��t��8������2��![]() ʱ��QP��AC��
ʱ��QP��AC��
��3����t=0.5s��2.5sʱֱ��QR������P��
��4��![]() ��t��0.5ʱ������PQMN��Rt��ABC�ڲ���
��t��0.5ʱ������PQMN��Rt��ABC�ڲ���
��������
�����������1����C��CD��ֱ��AB��D�㣬��AB��AQ�ij�������AB��AQ��ʾ��QB�ij���ֱ��������ABC���������������ֱ�DZ߳˻���һ�룬��б�߳���б���ϵĸߵ�һ�룬������ʾ�������ȿɵó�CD�ij���������BQC��QBΪ�ױߣ�CDΪ�ߣ����������ε������ʽ���������
��2����PQ��ACʱ��������ֱ��ƽ�еõ�����ͬλ����ȣ������Զ�Ӧ����ȵ������������Ƶõ���BPQ�ס�BCA�������Ƶñ����������Ե�ֵ�����г�����t�ķ��̣�������̵Ľ�õ�t��ֵ��
��3��������������ۼ��ɣ��ٵ�Q��P����AB��ʱ���ɵó�AP=6t��AQ=2+2t����AP=AQ�г�����t�ķ��̣�������̵Ľ�õ���ʱt��ֵ���ڵ�P��BC��ʱ����ͼ��ʾ����һ��ֱ����ȼ�һ�Թ�������ȣ��������Զ�Ӧ����ȵ������������ƿɵó�������BPQ��������ABC���ƣ������Ƶñ����������Ե�ֵ�����г�����t�ķ��̣�������̵Ľ�õ���ʱt��ֵ���۵�P��AC�ϲ�����QR������P�����ϣ��õ��������������t��ֵ��
��4��ץס�����ٽ����������P�ڵ�Q�����ʱ������N����AC�ϣ���PQ=2+2t��6t=2��4t���ɡ�APN�ס�ACB��![]() �������ʱ��tֵ������P�ڵ�Q���Ҳ�ʱ������N����BC�ϣ����ɡ�BPN�ס�BCA��
�������ʱ��tֵ������P�ڵ�Q���Ҳ�ʱ������N����BC�ϣ����ɡ�BPN�ס�BCA��![]() �����������ʱ��tֵ����������������ɵó���PQΪ����AB�Ϸ�������������PQMN��Rt��ABC�ڲ�ʱt��ȡֵ��Χ��
�����������ʱ��tֵ����������������ɵó���PQΪ����AB�Ϸ�������������PQMN��Rt��ABC�ڲ�ʱt��ȡֵ��Χ��
�����������1����C��CD��AB��D�㣬��ͼ��ʾ��

��AB=10��AQ=2+2t��
��QB=AB��AQ=10����2+2t��=8��2t��
��Rt��ABC��AB=10��AC=8��
���ݹ��ɶ����ã�BC=6��
��![]() AC��BC
AC��BC![]() AB��CD����
AB��CD����![]() ��6��8=
��6��8=![]() ��10��CD��
��10��CD��
��CD=![]() ��
��
��S��BCQ=![]() QBCD=
QBCD=![]() ��8��2t��=��
��8��2t��=��![]() t+
t+![]() ��0��t��8����
��0��t��8����
��2����PQ��ACʱ���ɵá�BPQ=��C����BQP=��A��
���BPQ�ס�BCA����BQ=8��2t��BP=6t��10��
��![]() ����
����![]() ��
��
�����ã�6��8��2t��=10��6t��10����
��ã�![]() ��
��
��![]() ʱ��QP��AC��
ʱ��QP��AC��

��3���ٵ�Q��P����AB��ʱ��AP=6t��AQ=2+2t��
�ɵã�AP=AQ����6t=2+2t��
��ã�t=0.5s��
�ڵ�P��BC��ʱ��P��R�غϣ���ͼ��ʾ��

�ߡ�PQB=��ACB=90�㣬��B=��B��
���BPQ�ס�BAC��
��![]() ����BP=6t��10��AB=10��BQ=8��2t��BC=6��
����BP=6t��10��AB=10��BQ=8��2t��BC=6��
��![]() ����6��6t��10��=10��8��2t����
����6��6t��10��=10��8��2t����
��ã�t=2.5s��
�۵�P��AC�ϲ�����QR������P��
���ϣ���t=0.5s��2.5sʱֱ��QR������P��
��4������P�ڵ�Q�����ʱ������N����AC�ϣ���ͼ��ʾ��

��AP=6t��AQ=2+2t��
��PQ=AQ��AP=2+2t��6t=2��4t��
���ı���PQMN�������Σ�
��PN=PQ=2��4t��
�ߡ�APN=��ACB=90�㣬��A=��A��
���APN�ס�ACB��
��![]() ����
����![]() ��
��
��ã�![]() ��
��
����P�ڵ�Q���Ҳ�ʱ������N����BC�ϣ���ͼ��ʾ��

������ã�BP=10��6t��PN=PQ=4t��2��
�ߡ�BPN=��BCA=90�㣬��B=��B��
���BPN�ס�BCA��
��![]() ����
����![]() ��
��
�����ã�8��10��6t��=6��4t��2����
��ã�![]() ��
��
��t=0.5ʱ��P���Q�غϣ�
��![]() ��t��0.5ʱ������PQMN��Rt��ABC�ڲ���
��t��0.5ʱ������PQMN��Rt��ABC�ڲ���