题目内容
【题目】一辆轿车从甲地出发开往乙地，同时，一辆客车从乙地开往甲地，一开始两车的速度相同，出发半小时后，客车因出现故障维修了一段时间，修好后为了不耽误乘客的时间，客车加快速度前进，结果与轿车同时到达各自的目的地．设轿车出发th后，与客车的距离为Skm，图中的折线（A→B→C→D→E）表示S与t之间的函数关系．
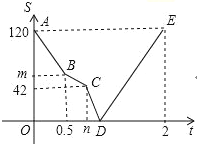
（1）甲、乙两地相距 km，轿车的速度为 km/h；
（2）求m与n的值；
（3）求客车修好后行驶的速度；
（4）求线段DE所对应的函数关系式，并注明自变量的取值范围．
【答案】（1）120，60；（2）m=60，n=0.8；（3）客车修好后行驶的速度为75（千米/时）．
（4）线段DE所对应的函数关系式为S=135t﹣150（
≤t≤2）．
【解析】
试题分析：（1）结合函数图象，可知当t=0时，S的值即为甲、乙两地之间的距离，再由“速度=路程÷时间”即可得出轿车的速度；
（2）根据B点的横坐标结合“两车间减少的距离=两车速度和×行驶时间”即可得出m的值，再由B、C两点间的纵坐标，利用“时间=纵坐标之差÷轿车的速度”可得出点B、C横坐标之差，再加上0.5即可得出n的值；
（3）由（2）可知客车修车耽误的时间，根据客车原来的速度可算出该时间段应该行驶的路程，将这段距离平摊到剩下的1.2小时中再加上原来的速度，即可得出客车修好后的速度；
（4）利用“时间=路程÷两车速度和”得出点C、D横坐标之差，结合点C的横坐标即可得出点D的坐标，设线段DE所对应的函数关系式为S=kt+b，根据点D、E的坐标利用待定系数法即可得出结论．
试题解析：（1）当t=0时，S=120，
故甲、乙两地相距为120千米；
轿车的速度为：120÷2=60（千米/时）．
故答案为：120；60．
（2）当t=0.5时，m=120﹣（60+60）×0.5=60．
在BC段只有轿车在行驶，
∴n=0.5+（60﹣42）÷60=0.8．
故m=60，n=0.8．
（3）客车维修的时间为：0.8﹣0.5=0.3（小时），
客车修好后行驶的速度为：0.3×60÷（2﹣0.8）+60=75（千米/时）．
（4）∵42÷（60+75）=
，
∴点D的横坐标为：0.8+
=
，
即点D的坐标为（
，0）．
设线段DE所对应的函数关系式为S=kt+b，
将点D（
，0）、点E（2，120）代入函数解析式得：
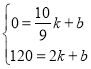，解得
．
∴线段DE所对应的函数关系式为S=135t﹣150（
≤t≤2）．
