��Ŀ����
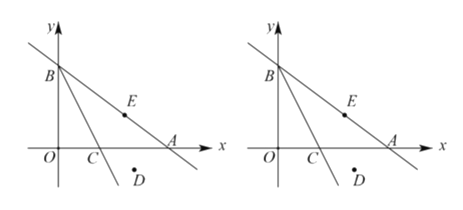
����Ŀ����ƽ��ֱ������ϵ�У���֪��A(x��y)����B(x��my��mx��y)������mΪ��������m��0�������B�ǵ�A�ġ�m�������㡱�����磺��A(1��2)�ġ�3�������㡱B������Ϊ(1��3��2��3��1��2)����B(��5��1)��
��1���㣨2��0���ġ�2�������㡱������Ϊ�� ����
��2������A�ġ�3�������㡱B��������(��1��5)�����A������Ϊ�� ����
��3������A(x��0)������x��0������A�ġ�m�������㡰Ϊ��B����AB��OA����m��ֵ��
��4������A(x��y)�ġ�m�������㡱�롰��m�������㡱������y��Գƣ����A��λ������ ����
���𰸡���1��(2��4)����2��(2��1)����3��m����1����4��y����
��������
��1��������m�����������Ķ������⣻
��2�����A����Ϊ��x��y����������m�����������Ķ����г������飬������⣻
��3���������A����m����������Ϊ��B��x��mx������AB��OA������⣻
��4���������A��x��y������m����������Ϊ��x��my��mx��y������A��x��y��������m����������Ϊ��x+my����mx��y��������ԳƵ����ʿ���x��0��������⣮
�⣺��1���㣨2��0������2����������������Ϊ��2��2��0��2��2��0��������2��4����
�ʴ�Ϊ��2��4����
��2�����A������x��y����
������ɵã�![]() ��
��
��![]() ��
��
���A������2��1����
��3���ߵ�A��x��0����
���A����m������������B��x��mx����
��AB��|mx|��
��AB��OA��
��|x|��|mx|��
��m����1��
��4���ߵ�A��x��y����
���A��x��y������m������������x��my��mx��y������A��x��y��������m������������x+my����mx��y����
�ߵ�A��x��y������m����������������m����������������y��Գƣ�
��![]() ��
��
��x��0��
���A��y���ϣ�
�ʴ�Ϊ��y���ϣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�