题目内容
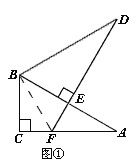
【题目】将两个全等的△ABC 和△DBE 按图 1 方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点 E 落在 AB 上,DE 所在直线交 AC 所在直线于点 F.
(1)若将图 1 中的△DBE 绕点 B 按顺时针方向旋转角α,且 0°<α<60°,其它条件不变,如图 2,请你直接写出线段 AF,EF,DE 的数量关系;
(2)若将图 1 中的△DBE 绕点 B 按顺时针方向旋转角β,且 60°≤β≤180°,其它条件不变.
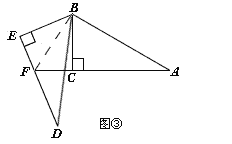
①如图 3,(1)中线段 AF,EF,DE 的数量关系是否仍然成立,若成立,请证明该结论;若不成立,请写出新的结论并证明.
②如图 4,AB 中点为 M,BE 中点为 N,若 BC= 2![]() ,连接 MN,当β= 度时,MN 长度最大,最大值为 (直接写出答案即可)
,连接 MN,当β= 度时,MN 长度最大,最大值为 (直接写出答案即可)

【答案】(1)AF+EF=DE;(2)①不成立.此时AF、EF与DE的关系为AF-EF=DE;②180,![]()
【解析】
(1)连接BF,由△ABC≌△DBE,可得BC=BE,根据直角三角形的HL判定全等即可得出答案;
(2)①同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,即可得出答案;②先利用三角形的三边关系,判断出点M,B,N在同一条直线上时,MN最大,即可得出答案.
解:(1)AF+EF=DE
连接BF(如图①),
∵△ABC≌△DBE,
∴BC=BE,AC=DE
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°,
∵BF=BF,
∴Rt△BFC≌Rt△BFE,
∴CF=EF,
又∵AF+CF=AC,
∴AF+EF=DE;
(2)①不成立.此时AF、EF与DE的关系为AF-EF=DE,
理由:连接BF(如图③),
∵△ABC≌△DBE,
∴BC=BE,AC=DE,
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°,
又∵BF=BF,
∴Rt△BFC≌Rt△BFE,
∴CF=EF,
又∵AF-CF=AC,
∴AF-EF=DE,
∴(1)中的结论不成立,正确的结论是AF-EF=DE
②在△BMN中,BN+BM>MN
∴点M,B,N在同一条直线上时
MN最大,最大值为BN+BM
即![]()
由(1)知,BE=BC=![]()
∵点N是BE的中点
∴BN=![]() BE=
BE=![]()
在RT△ABC中,∠A=30°,BC=![]()
∴AB=2BC=![]()
∵点M是AB的中点
∴BM=![]() AB=
AB=![]()
∴MN的最大值为:BN+BM=![]() =
=![]()
故答案为:180,![]() .
.

【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 480 | 601 | 1800 |
摸到白球的频率 |
|
|
|
|
|
|
|
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为______.
(2)试估算盒子里黑、白两种颜色的球各有多少个?

