题目内容
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.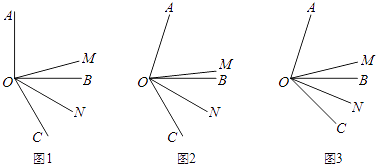
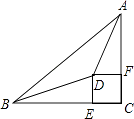
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
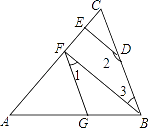
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
【答案】
(1)解:如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ![]() ∠AOC=75°,∠NOC=
∠AOC=75°,∠NOC= ![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°.
(2)解:如图2,∠MON= ![]() α,
α,
理由是:∵∠AOB=α,∠BOC=60°,
∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() α+30°,∠NOC=
α+30°,∠NOC= ![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=( ![]() α+30°)﹣30°=
α+30°)﹣30°= ![]() α.
α.
(3)解:如图3,∠MON= ![]() α,与β的大小无关.
α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (α+β),
(α+β),
∠NOC= ![]() ∠BOC=
∠BOC= ![]() β,
β,
∴∠AON=∠AOC﹣∠NOC=α+β﹣ ![]() β=α+
β=α+ ![]() β.
β.
∴∠MON=∠MOC﹣∠NOC
= ![]() (α+β)﹣
(α+β)﹣ ![]() β=
β= ![]() α
α
即∠MON= ![]() α.
α.
【解析】(1)由题意易求出∠AOC的度数,由OM平分∠AOC,ON平分∠BOC,可求得∠MOC和∠CON的度数,再由∠MON=∠MOC﹣∠NOC可求出;
(2)(3)解法同(1).

练习册系列答案
相关题目