题目内容
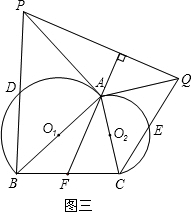
在△ABC中,分别以AB,AC为直径在△ABC外作半圆O1和半圆O2,其中O1和O2分别为两个半圆的圆心.F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
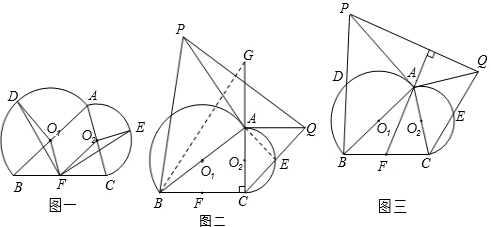
(1)如图一,连接O1F,O1D,DF,O2F,O2E,EF,证明:△DO1F≌△FO2E;
(2)过点A分别作半圆O1和半圆O2的切线,交BD的延长线和CE的延长线于点P和点Q,连接PQ,①如图二,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;②如图三,若连接FA,猜想PQ与FA的位置关系,并说明你的结论.

(1)如图一,连接O1F,O1D,DF,O2F,O2E,EF,证明:△DO1F≌△FO2E;
(2)过点A分别作半圆O1和半圆O2的切线,交BD的延长线和CE的延长线于点P和点Q,连接PQ,①如图二,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;②如图三,若连接FA,猜想PQ与FA的位置关系,并说明你的结论.
分析:(1)利用三角形中位线定理以及平行线的性质推知∠BO1F=∠CO2F;然后根据平行四边形的对边相等、圆周角定理知O1F=AO2=O2E,O2F=AO1=O1D,∠BO1D=90°,∠CO2E=90°;最后利用图形上角间的和差关系求得∠DO1F=∠FO2E,由全等三角形的判定定理ASA证得△DO1F≌△FO2E;
(2)①延长CA至G,使AG=AQ,连接BG、AE,构建全等三角形△AQP≌△AGB;然后根据全等三角形的对应边相等可以求得PQ=BG;最后在直角三角形BCG中利用勾股定理知BG=2
,
即PQ=2
;
②PQ⊥AF.
(2)①延长CA至G,使AG=AQ,连接BG、AE,构建全等三角形△AQP≌△AGB;然后根据全等三角形的对应边相等可以求得PQ=BG;最后在直角三角形BCG中利用勾股定理知BG=2
| 26 |
即PQ=2
| 26 |
②PQ⊥AF.
解答:(1)证明:如图一,
∵O1,O2,F分别是AB,AC,BC边的中点,
∴O1F∥AC且O1F=AO2,O2F∥AB且O2F=AO1,
∴∠BO1F=∠BAC,∠CO2F=∠BAC,
∴∠BO1F=∠CO2F
∵点D和点E分别为两个半圆圆弧的中点,
∴O1F=AO2=O2E,O2F=AO1=O1D,∠BO1D=90°,∠CO2E=90°,
∴∠BO1D=∠CO2E.
∴∠DO1F=∠FO2E.
∴△DO1F≌△FO2E.
(2)解:①如图二,延长CA至G,使AG=AQ,连接BG、AE.
∵点E是半圆O2圆弧的中点,
∴AE=CE=3
∵AC为直径
∴∠AEC=90°,
∴∠ACE=∠EAC=45°,AC=
=3
,
∵AQ是半圆O2的切线,
∴CA⊥AQ,
∴∠CAQ=90°,
∴∠ACE=∠AQE=45°,∠GAQ=90°
∴AQ=AC=AG=3
同理:∠BAP=90°,AB=AP=5
∴CG=6
,∠GAB=∠QAP
∴△AQP≌△AGB.
∴PQ=BG
∵∠ACB=90°,
∴BC=
=4
∴BG=
=2
∴PQ=2
.
②PQ⊥AF.
∵O1,O2,F分别是AB,AC,BC边的中点,
∴O1F∥AC且O1F=AO2,O2F∥AB且O2F=AO1,
∴∠BO1F=∠BAC,∠CO2F=∠BAC,
∴∠BO1F=∠CO2F
∵点D和点E分别为两个半圆圆弧的中点,
∴O1F=AO2=O2E,O2F=AO1=O1D,∠BO1D=90°,∠CO2E=90°,
∴∠BO1D=∠CO2E.
∴∠DO1F=∠FO2E.
∴△DO1F≌△FO2E.
(2)解:①如图二,延长CA至G,使AG=AQ,连接BG、AE.
∵点E是半圆O2圆弧的中点,
∴AE=CE=3
∵AC为直径
∴∠AEC=90°,
∴∠ACE=∠EAC=45°,AC=
| AE2+CE2 |
| 2 |
∵AQ是半圆O2的切线,
∴CA⊥AQ,
∴∠CAQ=90°,
∴∠ACE=∠AQE=45°,∠GAQ=90°
∴AQ=AC=AG=3
| 2 |
同理:∠BAP=90°,AB=AP=5
| 2 |
∴CG=6
| 2 |
∴△AQP≌△AGB.
∴PQ=BG
∵∠ACB=90°,
∴BC=
| AB2-AC2 |
| 2 |
∴BG=
| GC2+BC2 |
| 26 |
∴PQ=2
| 26 |
②PQ⊥AF.
点评:本题综合考查了切线的性质、勾股定理以及全等三角形的判定与性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
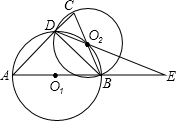 如图,在△ABC中,分别以AB、BC为直径的⊙O1、⊙O2交于AC上一点D,且⊙O1经过点O2,AB、DO2的延长线交于点E,且BE=BD.则下列结论不正确的是( )
如图,在△ABC中,分别以AB、BC为直径的⊙O1、⊙O2交于AC上一点D,且⊙O1经过点O2,AB、DO2的延长线交于点E,且BE=BD.则下列结论不正确的是( )| A、AB=AC | ||
| B、∠BO2E=2∠E | ||
C、AB=
| ||
D、EO2=
|
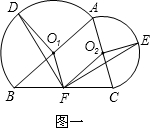
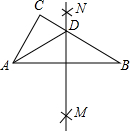 (2012•大田县质检)如图,在△ABC中,分别以点A和点B为圆心,大于
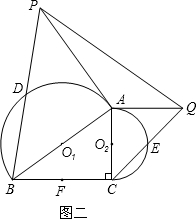
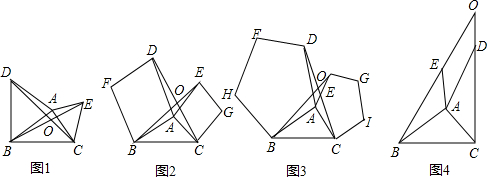
(2012•大田县质检)如图,在△ABC中,分别以点A和点B为圆心,大于 如图,在△ABC中,分别以AC,AB,BC为边向外作正方形,面积分别记为S1,S2,S3,若S1=6,S2=6,S3=12,则△ABC的形状是
如图,在△ABC中,分别以AC,AB,BC为边向外作正方形,面积分别记为S1,S2,S3,若S1=6,S2=6,S3=12,则△ABC的形状是