Question

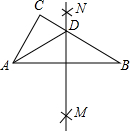（2012•大田县质检）如图，在△ABC中，分别以点A和点B为圆心，大于

1

2

AB的长为半径画弧，两弧交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为12，AB=16，则△ABC的周长为

28

．

Answer 1

分析：首先根据线段垂直平分线的性质可得AD=BD，再根据△ADC的周长为12可得AC+BC=12，再有条件AB=16可得△ABC的周长．

解答：解：由题意得：MN是线段AB的垂直平分线，
则AD=BD，
∵△ADC的周长为12，
∴AC+CD+AD=12，
∴AC+CD+DB=12，
即：AC+BC=12，
∵AB=16，
∴△ABC的周长为：AC+BC+AB=12+16=28，
故答案为：28．

点评：此题主要考查了线段垂直平分线的性质，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．