题目内容
如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t(0<t≤4).(1)写出△PBQ的面积S(cm2)与时间t(s)之间的函数表达式,当t为何值时,S有最
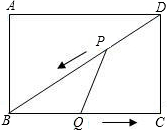 大值,最大值是多少?
大值,最大值是多少?(2)当t为何值时,△PBQ为等腰三角形?
(3)△PBQ能否成为等边三角形?若能,求t的值;若不能,说明理由.
分析:(1)△BPQ中,可根据Q的速度用时间t表示出底边BQ的长,而BQ边上的高,可用BP•sinPBQ来表示,根据三角形的面积公式即可求出S、t的函数关系式,根据函数的性质即可得出S的最大值.
(2)本题要分情况讨论:
①PB=BQ,可用t表示出BP,BQ的长,即可根据题设的等量关系求出t的值.
②PQ=BQ,过P作BD的垂线,设垂足为N,那么BN=
,然后在直角三角形BQN中,用BN的长和∠DBC的正弦值表示出BN联立前面BN的表达式即可求出t的值.
③PB=PQ,过P作PM⊥BQ与M,解法同②类似.
(3)如果三角形BPQ为等边三角形,必为(2)题三种条件中的一种,然后按(2)的条件判断三边是否相等即可.
(其实本题可直接得出△PBQ不是等边三角形,因为∠PBQ不可能是60°).
(2)本题要分情况讨论:
①PB=BQ,可用t表示出BP,BQ的长,即可根据题设的等量关系求出t的值.
②PQ=BQ,过P作BD的垂线,设垂足为N,那么BN=
| BP |
| 2 |
③PB=PQ,过P作PM⊥BQ与M,解法同②类似.
(3)如果三角形BPQ为等边三角形,必为(2)题三种条件中的一种,然后按(2)的条件判断三边是否相等即可.
(其实本题可直接得出△PBQ不是等边三角形,因为∠PBQ不可能是60°).
解答:解:(1)如图1,自点P向BC引垂线,垂足为M,则PM∥DC,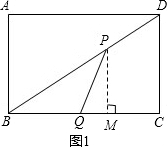
∴
=
.
∵DC=AB=3,BC=4,
∴BD=
=
=5.
当P,Q运动t秒后,
DP=BQ=1•t=t,BP=5-t.
∴PM=
=
=
.
∴S△PBQ=
•BQ•PM=
•t•
=-
(t-
)2+
.
∵0<t≤4,
∴当t=
时,S取得最大值,最大值为
.
(2)若△BPQ是等腰三角形.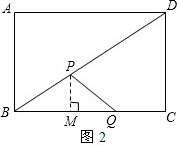
①如图2,当PB=PQ时,自点P向BC引垂线,垂足为M,则有BM=MQ.
方法一:
由△BMP∽△BCD,得
=
,
∴BM=
=
=
.
∴
=
,
解得t=
.
方法二:
在Rt△BMP中,BP=5-t,BM=
,cos∠DBC=
=
=
.
∴
=
,
解得t=
.
②当BQ=BP时,有t=5-t,解得t=
.
③如图3,当BQ=PQ时,自点Q向BD引垂线,垂足为N.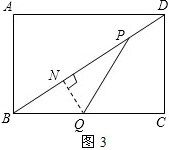
由Rt△BNQ∽Rt△BCD,
得
=
.
∴
=
,
解得t=
.
(3)不能.
若△PBQ为等边三角形,则BQ=BP=PQ.
由(2)②,知当BQ=BP时,t=
.
由(2)①,知当BP=PQ时,t=
.
∴BQ=BP与BP=PQ不能同时成立,∴△PBQ不可能为等边三角形.

∴
| PM |
| DC |
| BP |
| BD |
∵DC=AB=3,BC=4,
∴BD=
| BC2+DC2 |
| 42+32 |
当P,Q运动t秒后,
DP=BQ=1•t=t,BP=5-t.
∴PM=
| BP•DC |
| BD |
| (5-t)•3 |
| 5 |
| 15-3t |
| 5 |
∴S△PBQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 15-3t |
| 5 |
| 3 |
| 10 |
| 5 |
| 2 |
| 15 |
| 8 |
∵0<t≤4,
∴当t=
| 5 |
| 2 |
| 15 |
| 8 |
(2)若△BPQ是等腰三角形.

①如图2,当PB=PQ时,自点P向BC引垂线,垂足为M,则有BM=MQ.
方法一:
由△BMP∽△BCD,得
| BM |
| BC |
| BP |
| BD |
∴BM=
| BP•BC |
| BD |
| (5-t)•4 |
| 5 |
| 20-4t |
| 5 |
∴
| 20-4t |
| 5 |
| t |
| 2 |
解得t=
| 40 |
| 13 |
方法二:
在Rt△BMP中,BP=5-t,BM=
| t |
| 2 |
| BM |
| BP |
| BC |
| BD |
| 4 |
| 5 |
∴
| ||
| 5-t |
| 4 |
| 5 |
解得t=
| 40 |
| 13 |
②当BQ=BP时,有t=5-t,解得t=
| 5 |
| 2 |
③如图3,当BQ=PQ时,自点Q向BD引垂线,垂足为N.

由Rt△BNQ∽Rt△BCD,
得
| BN |
| BC |
| BQ |
| BD |
∴
| ||
| 4 |
| t |
| 5 |
解得t=
| 25 |
| 13 |
(3)不能.
若△PBQ为等边三角形,则BQ=BP=PQ.
由(2)②,知当BQ=BP时,t=
| 5 |
| 2 |
由(2)①,知当BP=PQ时,t=
| 40 |
| 13 |
∴BQ=BP与BP=PQ不能同时成立,∴△PBQ不可能为等边三角形.
点评:本题是点的运动型问题,考查了矩形的性质、二次函数的应用、等腰三角形的判定等知识点.
(2)题在不确定等腰三角形的腰和底边的情况下要分类讨论.
(2)题在不确定等腰三角形的腰和底边的情况下要分类讨论.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )



 .
. 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( ) DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.