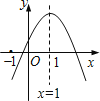题目内容
【题目】在平面直角坐标系
中，抛物线
与
轴交于点A，将点A向右平移2个单位长度，得到点B，点B在抛物线上．
（1） ①直接写出抛物线的对称轴是________；
②用含a的代数式表示b；
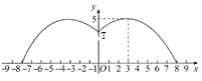
（2）横、纵坐标都是整数的点叫整点．点A恰好为整点，若抛物线在点A，B之间的部分与线段AB所围成的区域内（不含边界）恰有1个整点，结合函数的图象，直接写出a的取值范围．
【答案】（1）①直线x＝1；②b＝－2a；（2）－2≤a＜－1或1＜a≤2．
【解析】
(1) ①根据抛物线的对称性可以直接得出其对称轴；②利用对称轴公式
进一步求解即可；
（2）分两种情况：①
，②
，据此依次讨论即可．
解：（1）①∵当x=0时，y=c，∴点A坐标为（0，c），
∵点A向右平移2个单位长度，得到点B，∴点B（2，c），
∵点B在抛物线上，∴抛物线的对称轴是：直线x=1；
故答案为：直线x=1；
②∵抛物线的对称轴是直线：x=1，∴
，即
；
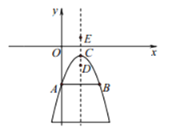
（2）①如图，若，
因为点A（0，c），B（2，c）都是整点，且指定区域内恰有一个整点，因此这个整点D的坐标必为（1，c－1），但是从运算层面如何保证“恰有一个”呢，与抛物线的顶点C（1，c－a）做位置与数量关系上的比较，必须考虑到紧邻点D的另一个整点E（1，c－2）不在指定区域内，所以可列出不等式组：
，解得：
；
②如图，若，
同理可得：
，解得：
；
综上所述，符合题意的a的取值范围是－2≤a<－1或1<a≤2．
【题目】北京市第十五届人大常委会第十六次会议表决通过《关于修改<北京市生活垃圾管理条例>的决定》，规定将生活垃圾分为厨余垃圾、可回收物、有害垃圾、其它垃圾四大基本品类，修改后的条例将于2020年5月1日实施 .某小区决定在2020年1月到3月期间在小区内设置四种垃圾分类厢：厨余垃圾、可回收物、有害垃圾、其它垃圾，分别记为A、B、C、D，进行垃圾分类试投放，以增强居民垃圾分类意识.
（1）小明家按要求将自家的生活垃圾分成了四类，小明从分好类的垃圾中随机拿了一袋，并随机投入一个垃圾箱中，请用画树状图的方法求垃圾投放正确的概率；
（2）为调查居民生活垃圾分类投放情况，现随机抽取了该小区四类垃圾箱中共1 000千克生活垃圾，数据统计如下（单位：千克）：
A | B | C | D | |
厨余垃圾 | 400 | 100 | 40 | 60 |
可回收物 | 25 | 140 | 20 | 15 |
有害垃圾 | 5 | 20 | 60 | 15 |
其它垃圾 | 25 | 15 | 20 | 40 |
求“厨余垃圾”投放正确的概率.
