题目内容
【题目】问题的提出:
如果点![]() 是锐角
是锐角![]() 内一动点,如何确定一个位置,使点
内一动点,如何确定一个位置,使点![]() 到△ABC的三顶点的距离之和
到△ABC的三顶点的距离之和![]() 的值为最小?
的值为最小?
(1)问题的转化:
把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
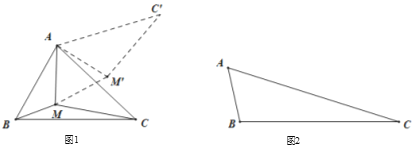
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() .
.
(2)问题的解决:
当点![]() 到锐角
到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 的度数.
的度数.
问题的延伸:
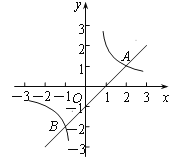
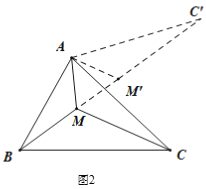
(3)如图2所示,在钝角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是这个三角形内一动点,请你利用以上方法,求点
是这个三角形内一动点,请你利用以上方法,求点![]() 到这个三角形各顶点的距离之和的最小值.
到这个三角形各顶点的距离之和的最小值.
【答案】(1)证明见解析;(2)∠AMB=120°;(3)![]() .
.
【解析】
(1)证明△AMM'是等边三角形,求出MM'=MA,结合MC=M'C'可得结论;
(2)当B、M、M'、C'在同一直线上时,MA+MB+MC的值为最小,此时∠AMM'=60°,故可得∠AMB=120°;
(3)根据题意作出辅助线,利用旋转的性质求出![]() ,求得
,求得![]() 和
和![]() 的长,然后在
的长,然后在![]() 中,利用勾股定理求出
中,利用勾股定理求出![]() 的长即可.
的长即可.
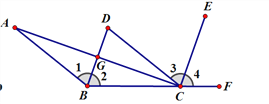
(1)如图1,由旋转的性质得:∠MAM'=60°,MA=M'A,
∴△AMM'是等边三角形,
∴MM'=MA,
∵MC=M'C',
∴MA+MB+MC=BM+MM′+M′C′;
(2)如图2,把△AMC绕点A逆时针旋转60度得到△AM′C′,连接MM′,由“问题的转化”可知:当B、M、M'、C'在同一直线上时,MA+MB+MC的值为最小,
由(1)可知△AMM'是等边三角形,则∠AMM'=60°,
∴∠AMB=120°;
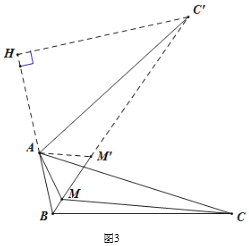
(3)如图3,把△AMC绕点A旋转60度得到△AM′C′,且B、M、M'、C'在同一直线上,过点![]() 作
作![]() 延长线的垂线
延长线的垂线![]() ,垂足为
,垂足为![]() ,
,
由旋转可得![]() ≌
≌![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵点B、M、M'、C'在同一直线上,
∴在![]() 中,
中,![]() ,
,
即点![]() 到这个三角形各顶点的距离之和的最小值为
到这个三角形各顶点的距离之和的最小值为![]() .
.

练习册系列答案
相关题目