题目内容
已知Rt△ABC中,∠ACB=90°,AB=5,两直角边AC、BC的长是关于x的方程x2-(m+5)x+6m=0的两个实数根.求m的值及AC、BC的长(BC>AC).
解:∵AC、BC的长是关于x的方程x2-(m+5)x+6m=0的两个实数根,
∴AC+BC=m+5,AC•BC=6m.
又AC2+BC2=AB2=25,
∴(m+5)2-2×6m=25,
即m2-2m=0,
m=2或m=0(不合题意,应舍去).
当m=2时,有x2-7x+12=0,x=3或x=4.
又BC>AC,
∴BC=4,AC=3.
分析:根据一元二次方程根与系数的关系以及勾股定理,求得m的值,进而求得AC、BC的长.
点评:此题的综合性比较强,注意数形结合的思想,能够把根与系数的关系与勾股定理有机地结合起来.
要熟练对完全平方公式进行变形.
∴AC+BC=m+5,AC•BC=6m.
又AC2+BC2=AB2=25,
∴(m+5)2-2×6m=25,
即m2-2m=0,
m=2或m=0(不合题意,应舍去).
当m=2时,有x2-7x+12=0,x=3或x=4.
又BC>AC,
∴BC=4,AC=3.
分析:根据一元二次方程根与系数的关系以及勾股定理,求得m的值,进而求得AC、BC的长.
点评:此题的综合性比较强,注意数形结合的思想,能够把根与系数的关系与勾股定理有机地结合起来.
要熟练对完全平方公式进行变形.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
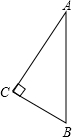 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点. 10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是
10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是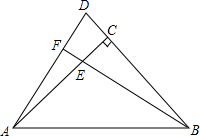 已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.