��Ŀ����
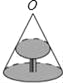
����Ŀ����ͼ����OΪԭ�㣬A��BΪ���������㣬AB��15����OA��OB��2��1����P�ӵ�B��ÿ��4����λ���ٶ������˶���
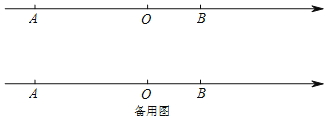
��1��A��B��Ӧ�����ֱ�Ϊ�� ������ ����
��2������P�˶�ʱ���ֱ�ȡBP���е�E��AO���е�F���뻭ͼ�������![]() ��ֵ��
��ֵ��
��3��������P��ʼ�˶�ʱ����A��B�ֱ���ÿ��2����λ��ÿ��5����λ���ٶ�ͬʱ�����˶����Ƿ���ڳ���m��ʹ��3AP+2OP��mBPΪ��ֵ�������ڣ������m��ֵ�Լ������ֵ���������ڣ���˵�����ɣ�
���𰸡���1����10��5����2����ͼ��������![]() ��2����3����m��14ʱ��Ϊ��ֵ55��
��2����3����m��14ʱ��Ϊ��ֵ55��
��������
��1������AB��15����OA��OB��2��1��ֱ�����OA��OB�ij��ȣ��Ӷ����A��B��Ӧ������
��2���������⻭ͼ���ɣ�Ȼ��![]() �ֱ���
�ֱ���![]() ��ʾ�������������ֵ.
��ʾ�������������ֵ.
��3���ֱ��ú�m�Ĵ���ʽ��ʾ��AP��OP��BP�������ж��Ƿ����mֵʹ3AP+2OP��mBPΪ��ֵ
��1����AB��15��OA��OB��2��1
��AO��10��BO��5
��A���Ӧ��Ϊ��10��B���Ӧ��Ϊ5��
�ʴ�Ϊ����10��5��
��2����ͼ���£�
![]()
����E��F�ֱ�ΪBP��AO���е�
��OF��![]() AO��BE��
AO��BE��![]() BP
BP
��EF��OF+OB+BE��![]() AO+OB+
AO+OB+![]() BP
BP
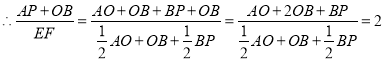
��3�����˶�ʱ��Ϊt�룬���P��Ӧ������5+4t����A��Ӧ��������10+2t����B��Ӧ������5+5t��
��AP��5+4t������10+2t����2t+15��OP��5+4t��BP��t��
��3AP+2OP��mBP��3��2t+15��+2��5+4t����mt����14��m��t+55��
����m��14ʱ��3AP+2OP��mBPΪ��ֵ55��

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�