题目内容
(本题满分12分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.

1.(1)求证:点E是边BC的中点;(4分)
2.(2)若EC=3,BD=![]() ,求⊙O的直径AC的长度;(4分)
,求⊙O的直径AC的长度;(4分)
3.(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由. (4分)
1.(1)证明:连接DO,
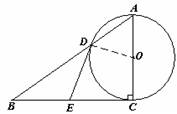
∵∠ACB=90°,AC为直径, ∴EC为⊙O的切线,
又∵ED也为⊙O的切线, ∴EC=ED. (2分)
又∵∠EDO=90°, ∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°,
又∵∠B+∠A=90° ∴∠BDE=∠B, ∴EB=ED.
∴EB=EC,即点E是边BC的中点.
2.(2)∵BC,BA分别是⊙O的切线和割线,
∴BC2=BD·BA, ∴(2EC)2= BD·BA,即BA·![]() =36,∴BA=
=36,∴BA=![]() , (6分)
, (6分)
在Rt△ABC中,由勾股定理得 AC=![]() =
=![]() =
=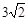 .
.
3.(3)△ABC是等腰直角三角形. (9分)
理由:∵四边形ODEC为正方形, ∴∠DOC=∠ACB=90°,即DO∥BC,
又∵点E是边BC的中点, ∴BC=2OD=AC,
∴△ABC是等腰直角三角形. (12分)
解析:略

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
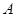 作
作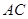 ∥
∥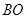 交上述函数图像于点
交上述函数图像于点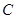 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)

 的长;
的长;
 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?

 ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
 时,求线段
时,求线段 的长;
的长; 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.