题目内容
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10 ![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为海里/小时?
【答案】10+10 ![]()
【解析】解:如图:乙沿南偏东30°方向航行则∠DOB=30°,甲沿南偏西75°方向航行,则∠AOD=75°,
当航行1小时后甲沿南偏东60°方向追赶乙船,则∠2=90°﹣60°=30°.
∵∠3=∠AOD=75°,
∴∠1=90°﹣75°=15°,
故∠1+∠2=15°+30°=45°.
过O向AB作垂线,则∠AOC=90°﹣∠1﹣∠2=90°﹣15°﹣30°=45°,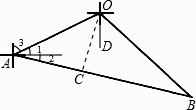
∵OA=10 ![]() ,∠OAB=∠AOC=45°,
,∠OAB=∠AOC=45°,
∴OC=AC=OAsin45°=10 ![]() ×
× ![]() =10.
=10.
在Rt△OBC中,∠BOC=∠AOD+∠BOD﹣∠AOC=75°+30°﹣45°=60°,
∴BC=OCtan60°=10 ![]() ,
,
∴AB=AC+BC=10+10 ![]() .
.
因为OC=10海里,∠B=30°,所以OB=2OC=2×10=20,
乙船从O到B所用时间为20÷10=2小时,
由于甲从O到A所用时间为1小时,则从A到B所用时间为2﹣1=1小时,
甲船追赶乙船的速度为10+10 ![]() 海里/小时.
海里/小时.
根据题意画图,过O向AB作垂线,根据特殊角的三角函数值求得AC、BC的值,从而求得AB的值.根据追及问题的求法求甲船追赶乙船的速度.

练习册系列答案
相关题目