题目内容
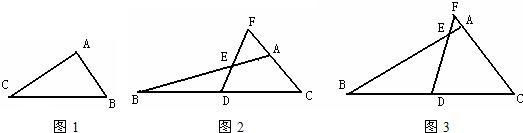 23、(1)如图1,在△ABC中,绕点C旋转180°后,得到△CA′B′请先画出变换后的图形,写出下列结论正确的序号是
23、(1)如图1,在△ABC中,绕点C旋转180°后,得到△CA′B′请先画出变换后的图形,写出下列结论正确的序号是①②③④
.①△ABC≌△A′B′C;
②线段AB绕C点旋转180°后,得到线段A′B′;
③A′B′∥AB;
④C是线段BB′的中点.
在(1)的启发下解答下面问题:
(2)如图2,在△ABC中,∠BAC=120°,D是BC的中点,射线DF交BA于E,交CA的延长线于F,请猜想∠F等于多少度时,BE=CF?(直接写出结果,不证明)
(3)如图3,在△ABC中,如果∠BAC≠120°,而(2)中的其他条件不变,若BE=CF的结论仍然成立,那么∠BAC与∠F满足什么数量关系(等式表示)并加以证明.
分析:(1)通过旋转的性质可知①②③④正确;
(2)通过正确作图,使BE=CF,然后进行测量即可进行猜想;
(3)通过旋转的方法,作出辅助线,可利用三角形全等或旋转的性质得到相等的线段,把关系转化到一个三角形中即可得到需要的条件.
(2)通过正确作图,使BE=CF,然后进行测量即可进行猜想;
(3)通过旋转的方法,作出辅助线,可利用三角形全等或旋转的性质得到相等的线段,把关系转化到一个三角形中即可得到需要的条件.
解答: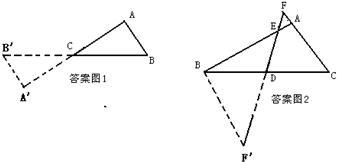 解:
解:
(1)根据旋转的性质,知①②③④都是正确的.
(2)60°.
(3)等量关系:∠BAC=2∠F.
作△FCD关于点D的中心对称三角形DBF′,则
∠F′=∠F,FC=BF′=BE,∠F′=∠F=∠BED=∠FEA.
∴∠BAC=2∠F.
 解:
解:(1)根据旋转的性质,知①②③④都是正确的.
(2)60°.
(3)等量关系:∠BAC=2∠F.
作△FCD关于点D的中心对称三角形DBF′,则
∠F′=∠F,FC=BF′=BE,∠F′=∠F=∠BED=∠FEA.
∴∠BAC=2∠F.
点评:本题考查旋转的性质和中心对称的特点.
旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意中心对称是旋转的一种特殊情况.
旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意中心对称是旋转的一种特殊情况.

练习册系列答案
相关题目

 图2,中间会出现一个小孔,如果正方形ABCD的边长为a,试计算图2中小孔的面积.
图2,中间会出现一个小孔,如果正方形ABCD的边长为a,试计算图2中小孔的面积.