题目内容
如图1，在一个7×7的正方形ABCD网格中，实线将它分割成5块，再把这5块拼成如
图2，中间会出现一个小孔，如果正方形ABCD的边长为a，试计算图2中小孔的面积．
分析：连接AE，则可求出△AEF的面积，然后也能得出△AED的面积，根据图形可求出GE的长度，然后根据拼成如图2，中间会出现一个小孔可求出小孔的面积．
解答：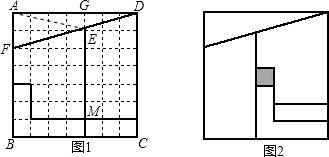
解：如图，连接AE，则S△AEF=
•
•
=
，
S△AED=S△ADF-S△AEF=
，
∴GE=
，
∴EM=GM-GE=
，
∴小孔面积S=a(
a+
a)-a2=
a2．
解：如图，连接AE，则S△AEF=| 1 |
| 2 |
| 2a |
| 7 |
| 4a |
| 7 |
| 4a2 |
| 49 |
S△AED=S△ADF-S△AEF=
| 3a2 |
| 49 |
∴GE=
| 6a |
| 49 |
∴EM=GM-GE=
| 36a |
| 49 |
∴小孔面积S=a(
| 2 |
| 7 |
| 36 |
| 49 |
| 1 |
| 49 |
点评：本题考查面积及等积变换，难度较大，解答本题的关键是正确作出辅助线，利用面积求出GE的长是本题的突破口．
练习册系列答案
阅读快车系列答案
相关题目
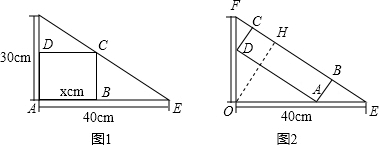
（2013•白下区一模）问题：如图，要在一个矩形木板ABCD上切割、拼接出一个圆形桌面，可在该木板上切割出半径相等的半圆形O1和半圆形O2，其中O1、O2分别是AD、BC上的点，半圆O1分别与AB、BD 相切，半圆O2分别与CD、BD相切．若AB=am，BC=bm，求最终拼接成的圆形桌面的半径（用含a、b的代数式表示）．
（2012•呼和浩特）如图是交警在一个路口统计的某个时段来往车辆的车速情况（单位：千米/时）