题目内容
【题目】如图,在直角坐标系中,直线y=﹣![]() x+
x+![]() 与x轴交于点A,与y=﹣
与x轴交于点A,与y=﹣![]() x相交于点B,点C是线段OB上一动点,连接AC,在AC上方取点D,使得cos∠CAD=
x相交于点B,点C是线段OB上一动点,连接AC,在AC上方取点D,使得cos∠CAD=![]() ,且
,且![]() =
=![]() ,连接OD,当点C从点O运动到点B时,线段OD扫过的面积为_____.
,连接OD,当点C从点O运动到点B时,线段OD扫过的面积为_____.
【答案】![]() .
.
【解析】
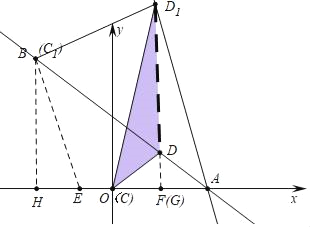
首先说明:当点C与B重合时,点D位于D1,此时AD1=![]() ,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积;
,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积;
解:∵直线y=﹣![]() x+
x+![]() 与x轴交于点A,
与x轴交于点A,
∴A(7,0),
由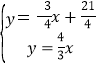 解得
解得![]() ,
,
∴B(﹣9,12),
作BH⊥x轴于H,则BH=12,OH=9,AH=16,
∴AB=![]() =20,
=20,
∴cos∠BAO=![]() ,
,
∵cos∠CAD=![]() ,
,
∴∠BAO=∠CAD,
当点C与O重合时,点D在线段AB上,
∵OA=7,OA:AD=7:5,
∴AD=5,作DF⊥OA于F,
∴DF=3,AF=4,OF=3,D(3,3),
当点C与B重合时,点D位于D1,此时AD1=![]() ,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积,
,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积,
在AH上取一点E,使得AE=BE,设AE=BE=x,
在Rt△BHE中,x2=122+(16﹣x)2,
∴x=![]() ,
,
∴BE=AE=![]() ,HE=
,HE=![]() ,作D1G⊥OA于G.
,作D1G⊥OA于G.
∵∠BAD1=∠BAO,∠BAO=∠EBA,
∴∠BEH=∠GAD1,
∴△BHE∽△D1GA,
∴![]() ,
,
∴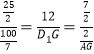 ,
,
∴D1F=![]() ,AG=4,
,AG=4,
∴OG=3(点F与G重合),
∴D1(3,![]() ),∵D(3,3),
),∵D(3,3),
∴DD1∥y,
∴![]() =
=![]() .
.
故答案是:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目