题目内容
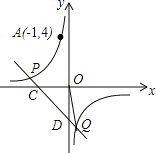
【题目】如图,反比例函数![]() 上的图象经过点
上的图象经过点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
![]() 求k的值;
求k的值;
![]() 连接OQ,是否存在实数b,使得
连接OQ,是否存在实数b,使得![]() ?若存在,请求出b的值;若不存在,请说明理由.
?若存在,请求出b的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() 的值为
的值为![]() .
.
【解析】
(1)根据反比例函数的图象上点的坐标特征易得k=-4;
(2)先表示出C(b,0),根据三角形面积公式,由于S△ODQ=S△OCD,所以点Q和点C到OD的距离相等,则Q的横坐标为(-b,0),利用直线解析式可得到Q(-b,2b),再根据反比例函数的图象上点的坐标特征得到-b2b=-4,然后解方程即可得到满足条件的b的值.
![]() 反比例函数
反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
![]() ;
;
![]() 存在.
存在.
当![]() 时,
时,![]() ,解得
,解得![]() ,则
,则![]() ,
,
![]() ,
,
![]() 点Q和点C到OD的距离相等,
点Q和点C到OD的距离相等,
而Q点在第四象限,
![]() 的横坐标为
的横坐标为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() 点Q在反比例函数
点Q在反比例函数![]() 的图象上,
的图象上,
![]() ,解得
,解得![]() 或
或![]() 舍去
舍去![]() ,
,
![]() 的值为
的值为![]() .
.

练习册系列答案
相关题目







