题目内容
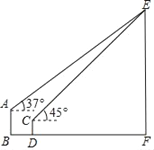
【题目】如图,甲楼AB高20m,乙楼CD高10m,两栋楼之间的水平距离BD=20m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
【答案】电视塔的高度EF约为110m.
【解析】
作AM⊥EF、CN⊥EF,设EN=xm,由∠ECN=45°知CN=EN=xm,根据BD=20m、AB=MF=10m、CD=NF=10m可得AM=x+20、EM=x﹣10,由tan∠EAM=![]() 列出关于x的方程,解之求得x的值即可得.
列出关于x的方程,解之求得x的值即可得.
如图所示,过点A作AM⊥EF于点M,过点C作CN⊥EF于点N,
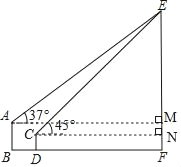
设EN=xm,
∵∠ECN=45°,
∴CN=EN=xm,
∵BD=20m,AB=MF=10m,CD=NF=10m,
∴AM=BF=BD+DF=BD+CN=x+20(m),EM=EN﹣MN=EN﹣(MF﹣NF)=x﹣10(m),
∵tan∠EAM=![]() ,
,
∴![]() =0.75,
=0.75,
解得:x=100,
则EF=110m,
答:电视塔的高度EF约为110m.

练习册系列答案
相关题目