题目内容
【题目】如图，在平面直角坐标系中，已知点A（0，1），直线l：y=﹣1．动点P满足条件：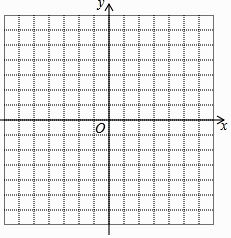
①P在这个平面直角坐标系中；
②P到A的距离和P到l的距离相等；
（1）求点P所经过的轨迹方程，并在网格中绘制这个图象．（提示：平面直角坐标系中两点之间的距离可以通过勾股定理来求得）
（2）已知直线y=kx+1，小明同学说，这条直线与（1）中所绘的图象有两个交点？你能说明小明为什么这么说吗？
（3）经过了上述的计算、绘图，小明发现，如果第（2）问的两个交点分别为B、C，那么，过BC的中点M作直线l的垂线，垂足为H，连接BH、CH，所得到的三角形BCH是个特殊的三角形，你能说明它是什么三角形吗？为什么？
【答案】
（1）
解：设P的坐标为P（x，y），由题意得： 
=|y+1|，
两边平方得：x2+（y﹣1）2=（y+1）2，
∴y= 
x2，即P的轨迹为一抛物线，其图象如图1所示；
（2）
解：抛物线直线方程联立得 
，消去y可得x2﹣4kx﹣4=0，
∴△=16k2+16＞0，
∴直线y=kx+1与抛物线有两个交点；
（3）
解：如图2，过B作BB′⊥l于B′，过C作CC′⊥l于C′，
由（1）中的条件可得BB′=BA，CC′=CA，
∴BC=BA+AC=BB′+CC′，
又由题意可得MH是梯形BB′C′C的中位线，
∴MH= 
（BB′+CC′）= BC，
∴MB=MC=MH，
∴△BHC是以∠BHC为直角的直角三角形．
【解析】（1）设出P点坐标，表示出P到A的距离和P到l的距离相等，可求得其轨迹方程，可画出图象；（2）联立直线与抛物线解析式利用一元二次方程的判别式可判断得出；（3）过B作BB′⊥l于B′，过C作CC′⊥l于C′，由条件可证明MH为梯形BB′C′C的中位线，可证得△BCH为直角三角形．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
